Exercises

Mikołaj Bojańczyk

Idempotent semigroup. Call a semigroup idempotent if every element is idempotent.

0. Show that if a semigroup is idempotent and $\Jj$ -trivial, then it is commutative.

1. Prove that if a semigroup is idempotent, then every $\Jj$ -class is closed under multiplication (i.e. it is a sub-semigroup)

2. Prove that for every $n$ there are finitely many idempotent semigroups with $n$ generators.

Strongly connected automata. Let $L \subseteq \Sigma^*$ be a regular language with the following properties:

the minimal DFA is strongly connected (i.e. every state is reachable from every other state);
the minimal DFA of the reverse of 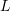$L$ is strongly connected;
the syntactic monoid of 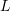$L$ is aperiodic.

Prove that $L$ is trivial, i.e. empty or full.