9. Countable scattered chains
Chains and total orders. A total order is a set ![]() together with an ordering
together with an ordering ![]() which is total (also known as linear) in the sense that every two elements are comparable. Define a chain over an alphabet
which is total (also known as linear) in the sense that every two elements are comparable. Define a chain over an alphabet ![]() to be a nonempty totally ordered set with a labelling of its elements by
to be a nonempty totally ordered set with a labelling of its elements by ![]() . We consider chains up to isomorphism, i.e. we identify two chains if there is a bijection between their positions that preserves the order and labelling. We write
. We consider chains up to isomorphism, i.e. we identify two chains if there is a bijection between their positions that preserves the order and labelling. We write ![]() for the (class) of all chains over the alphabet
for the (class) of all chains over the alphabet ![]() .
.
There is a natural monad structure on chains. If ![]() is a function on alphabets, then its lifting to chains
is a function on alphabets, then its lifting to chains
![]()
is defined coordinate-wise in the obvious way, by keeping positions unchanged and applying ![]() only to the labels. The unit operation
only to the labels. The unit operation
![]()
sends a label to the one-element chain with this label, and the flattening operation
![]()
defined in the natural way. The formal definition of flattening involves lexicographic product of orderings. One can check that all axioms of a monad are satisfied.
There are two problems with the chain monad defined above. The first problem is that ![]() is not a set, but a class. The second problem is that the algebras for this monad can be very complicated. A corollary of a result of Shelah is that there are algebras with finite universes over this monad where it is undecidable if an element is generated by a set of other elements. (A precise formulation of this result would require some space, not to mention the proof, and is omitted.) For these vaguely sketched reasons, we will concentrate on submonads of the chain monads, where not all chains are used. We will consider the following special cases, all of which are countable chains: finite chains, countable chains that are well-founded, countable chains that are scattered, and finally all countable chains.
is not a set, but a class. The second problem is that the algebras for this monad can be very complicated. A corollary of a result of Shelah is that there are algebras with finite universes over this monad where it is undecidable if an element is generated by a set of other elements. (A precise formulation of this result would require some space, not to mention the proof, and is omitted.) For these vaguely sketched reasons, we will concentrate on submonads of the chain monads, where not all chains are used. We will consider the following special cases, all of which are countable chains: finite chains, countable chains that are well-founded, countable chains that are scattered, and finally all countable chains.
The case of finite chains is the case of semigroups. The remaining cases are studied in the following lectures. We begin with scattered countable chains, and their special case of well-founded countable chains.
Scattered chains.
Call a chain scattered if one cannot remove positions and end up with a chain indexed by the rational numbers. For example, any chain indexed by the integers is scattered. The following lemma, whose straightforward proof is omitted, says that scattered chains (also, countable chains and well-founded chains) are closed under the flattening operation as defined for the monad of chains.
Lemma. If ![]() is scattered, and every position of
is scattered, and every position of ![]() is labelled by a scattered chain, then also the flattening of
is labelled by a scattered chain, then also the flattening of ![]() is scattered. Same for countable and well-founded chains.
is scattered. Same for countable and well-founded chains.
A corollary of the above lemma is that if we define ![]() to be the restriction of the chain monad
to be the restriction of the chain monad ![]() to scattered countable chains, with the unit and flattening restricted to the smaller domain of scattered countable chains, then it is also a monad. In this sense,
to scattered countable chains, with the unit and flattening restricted to the smaller domain of scattered countable chains, then it is also a monad. In this sense, ![]() is a submonad of
is a submonad of ![]() .
.
Theorem. A ![]() -algebra
-algebra ![]() with finite universe
with finite universe ![]() is uniquely determined by the values of its multiplication operation on structures of the form
is uniquely determined by the values of its multiplication operation on structures of the form
![]()
Proof. In the proof of this theorem, we pay pedantic attention to the distinction between a chain of chains and its flattening. In later proofs, we will not be so precise. If ![]() are chains in
are chains in ![]() , then we write
, then we write ![]() for the chain of chains which has
for the chain of chains which has ![]() positions, where the
positions, where the ![]() -th position is labelled by
-th position is labelled by ![]() . To get the actual concatenation of these chains, we need to apply the flattening operation. Likewise, we write
. To get the actual concatenation of these chains, we need to apply the flattening operation. Likewise, we write ![]() for an
for an ![]() -chain of chains.
-chain of chains.
The key lemma is Hausdorff’s theorem, which characterizes countable scattered chains as those that can be constructed from singleton chains using concatenation indexed by the two-element chain, ![]() or the reverse of
or the reverse of ![]() . The theorem says that for every set of labels
. The theorem says that for every set of labels ![]() , one can assign ordinal numbers (call them Hausdorff ranks) to
, one can assign ordinal numbers (call them Hausdorff ranks) to ![]() , such that for every chain
, such that for every chain ![]() with at least two positions there exists a decomposition of at least one of three types listed below:
with at least two positions there exists a decomposition of at least one of three types listed below:
(1) 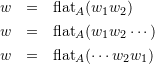
such that the chains ![]() on the right side have strictly smaller rank than
on the right side have strictly smaller rank than ![]() .
.
We now proceed with the proof of the theorem. Let ![]() be a finite set. We need to show that if we have two Eilenberg-Moore algebras with this universe, which have multiplication operations
be a finite set. We need to show that if we have two Eilenberg-Moore algebras with this universe, which have multiplication operations
![]()
that agree on the structures mentioned in the statement of the theorem, then the two multiplication operations are the same.
When ![]() is a chain of size one, then both
is a chain of size one, then both ![]() and
and ![]() need to be the label used in the chain, by the axiom of Eilenberg-Moore algebras which says that multiplication composed with the unit must be the identity.
need to be the label used in the chain, by the axiom of Eilenberg-Moore algebras which says that multiplication composed with the unit must be the identity.
Suppose now that ![]() is a chain of size at least two. We will prove that
is a chain of size at least two. We will prove that
![]()
by induction on the Hausdorff rank of ![]() .
.
Let us first consider the case when ![]() admits a decomposition
admits a decomposition
![]()
In this case we simply apply induction and use the assumption that the multiplication operations agree on chains of length two:
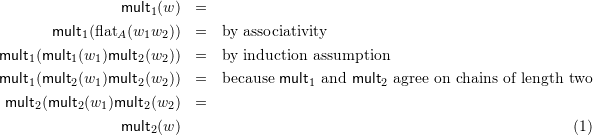
Consider now the case when ![]() admits a decomposition
admits a decomposition
![]()
Here we apply the Ramsey theorem. For numbers ![]() , define
, define
![]()
By induction assumption, and using the same argument as in the previous paragraph, we see that
![]()
Let us write ![]() for the element described by both sides of the above equality. By the Ramsey theorem, there is some infinite set of natural numbers
for the element described by both sides of the above equality. By the Ramsey theorem, there is some infinite set of natural numbers ![]() such that all
such that all ![]() with
with ![]() are the same element, call it
are the same element, call it ![]() . Using associativity, we see that
. Using associativity, we see that
![]()
Since the right side only depends on arguments where ![]() and
and ![]() are known to agree, the result follows.
are known to agree, the result follows.
The same proof as in the previous paragraph is used for the last kind of decomposition, indexed by reverse ![]() .
. ![]()
Well-founded chains. Call a chain well-founded if its set of positions is well founded. This is a special case of a scattered chain. As for scattered countable chains, countable well-founed chains form a monad, call it ![]() .
.
Theorem. A ![]() -algebra
-algebra ![]() is uniquely determined by the values of its multiplication operation on structures of the form
is uniquely determined by the values of its multiplication operation on structures of the form
![]()
Proof. The same proof as for the monad ![]() . When applying the Hausdorff theorem, we can never get a decomposition indexed by reverse
. When applying the Hausdorff theorem, we can never get a decomposition indexed by reverse ![]() , since this would contradict well-foundedness.
, since this would contradict well-foundedness. ![]()
Leave a Reply