7. Algebra for infinite words
Recall that a monoid consists of a universe ![]() together with a product operation
together with a product operation
![]()
which maps each one letter word ![]() to
to ![]() , and which is associative in the sense that the following diagram commutes
, and which is associative in the sense that the following diagram commutes
![Rendered by QuickLaTeX.com \[\xymatrix{(M^*)^* \ar[r]^{flat} \ar[d]_{\pi^*} & M^* \ar[d]^\pi \\ M^* \ar[r]_\pi & M}\]](https://www.mimuw.edu.pl/~bojan/wp-content/ql-cache/quicklatex.com-3d85961c181c602eea860017ed60428d_l3.png)
where ![]() flattens a word of words into a word in the obvious way, while
flattens a word of words into a word in the obvious way, while ![]() applies the product operation to every word in a word of words.
applies the product operation to every word in a word of words.
To define monoids for infinite words, we use the same definition, only ![]() is replaced by
is replaced by ![]() . This requires a new flattening operation
. This requires a new flattening operation
![]()
which we illustrate on three examples:
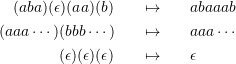
Note how in the second example above, the first infinite word causes the rest of the input to be ignored. This ignoring is a little bit of a hack, which could be avoided by either using two sorts (finite and infinite word), or by considering a richer notion of words which is closed under substitution, e.g. words where the positions form a countable well-ordering.
Summing up, ![]() -monoids are defined below.
-monoids are defined below.
Definition. An ![]() -monoid consists of a unierse
-monoid consists of a unierse ![]() together with a product operation
together with a product operation
![]()
which is the identity on one letter words and which is associative in the sense that the following diagram commutes
![Rendered by QuickLaTeX.com \[\xymatrix{(M^\infty)^\infty \ar[r]^{flat} \ar[d]_{\pi^\infty} & M^\infty \ar[d]^\pi \\ M^\infty \ar[r]_\pi & M}\]](https://www.mimuw.edu.pl/~bojan/wp-content/ql-cache/quicklatex.com-6d73dddb37c382bce083ec99314a3ee6_l3.png)
It is not difficult to see that ![]() , with flattening as the monoid operation, is an
, with flattening as the monoid operation, is an ![]() -monoid. Here is an example of an
-monoid. Here is an example of an ![]() -monoid with a finite universe.
-monoid with a finite universe.
Example. This ![]() -monoid is going to recognize the
-monoid is going to recognize the ![]() -words over alphabet
-words over alphabet ![]() which contain infinitely many
which contain infinitely many ![]() ‘s. The universe is
‘s. The universe is
![]()
The product operation is defined as follows. To define ![]() with
with ![]() , we do the following. First, remove all
, we do the following. First, remove all ![]() letters from
letters from ![]() . If the result is empty, return
. If the result is empty, return ![]() . If there is a letter of the form
. If there is a letter of the form ![]() or
or ![]() , then return the
, then return the ![]() or
or ![]() , whichever comes first in
, whichever comes first in ![]() . Otherwise, if the result is an infinite word, then return
. Otherwise, if the result is an infinite word, then return ![]() if there are infinitely many
if there are infinitely many ![]() ‘s and
‘s and ![]() otherwise. Otherwise, return
otherwise. Otherwise, return ![]() if there is at least one
if there is at least one ![]() and
and ![]() otherwise.
otherwise. ![]()
Homomorphism. Define a homomorphism of ![]() -monoids
-monoids ![]() and
and ![]() to be a function
to be a function ![]() between their universes which respects the structure of
between their universes which respects the structure of ![]() -morphisms in the sense that the following diagram commutes
-morphisms in the sense that the following diagram commutes
![Rendered by QuickLaTeX.com \[\xymatrix{M^\infty \ar[r]^{h^\infty} \ar[d]_{\pi_M} & N^\infty \ar[d]^{\pi_N} \\ M \ar[r]^h & N}\]](https://www.mimuw.edu.pl/~bojan/wp-content/ql-cache/quicklatex.com-e8c3a6f116e64797611530a400555694_l3.png)
Compositional functions. As with normal monoids, instead of defining an associative product operation on a universe ![]() , it is sometimes easier to give a compositional function from an existing
, it is sometimes easier to give a compositional function from an existing ![]() -monoid to
-monoid to ![]() , and get the
, and get the ![]() -monoid structure on
-monoid structure on ![]() automatically from that. We describe this now. Suppose that
automatically from that. We describe this now. Suppose that ![]() is an
is an ![]() -monoid and
-monoid and ![]() is a set. A function
is a set. A function
![]()
is called compositional if every words ![]() satisfy
satisfy
![]()
Lemma. If ![]() is compositional, then there is a multiplication operation on
is compositional, then there is a multiplication operation on ![]() which turns it into an
which turns it into an ![]() -monoid, and which turns
-monoid, and which turns ![]() into a homomorphism of
into a homomorphism of ![]() -monoids.
-monoids.
Proof. Compositionality can be rephrased as saying that there is some function ![]() which makes the following diagram commute
which makes the following diagram commute
![Rendered by QuickLaTeX.com \[\xymatrix{M^\infty \ar[r]^{h^\infty} \ar[d]_{\pi} & N^\infty \ar[d]^\sigma \\ M \ar[r]^h & N}\]](https://www.mimuw.edu.pl/~bojan/wp-content/ql-cache/quicklatex.com-b04a55594e5cea616c4ca246d9e041ae_l3.png)
The above diagram then shows that ![]() is a homomorphism, assuming that
is a homomorphism, assuming that ![]() yields a structure of an
yields a structure of an ![]() -monoid on
-monoid on ![]() , i.e. it is associative. Associativity is not difficult to show.
, i.e. it is associative. Associativity is not difficult to show. ![]()
Leave a Reply