Mikołaj Bojańczyk
Exercises
Idempotent semigroup. Call a semigroup idempotent if every element is idempotent.
0. Show that if a semigroup is idempotent and ![]() -trivial, then it is commutative.
-trivial, then it is commutative.
1. Prove that if a semigroup is idempotent, then every ![]() -class is closed under multiplication (i.e. it is a sub-semigroup)
-class is closed under multiplication (i.e. it is a sub-semigroup)
2. Prove that for every ![]() there are finitely many idempotent semigroups with
there are finitely many idempotent semigroups with ![]() generators.
generators.
Strongly connected automata. Let ![]() be a regular language with the following properties:
be a regular language with the following properties:
- the minimal DFA is strongly connected (i.e. every state is reachable from every other state);
- the minimal DFA of the reverse of
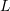 is strongly connected;
is strongly connected; - the syntactic monoid of
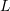 is aperiodic.
is aperiodic.
Prove that ![]() is trivial, i.e. empty or full.
is trivial, i.e. empty or full.
Leave a Reply