3. The Schützenberger Theorem

Mikołaj Bojańczyk

zajęcia / courses

The theorem is part of a bigger picture, which is the strong connection between automata, monoids and logic. It turns out that, when studying regular languages, the most natural logic is not the classical first-order logic, but a more expressive logic called monadic second-order logic, which has the same expressive power as regular languages. The Schützenberger theorem in this logic is best understood as part of this bigger picture: it explains the expressive power of first-order logic as a fragment of monadic-second order logic. Since monadic second-order logic is outside the scope of this lecture, we do not talk about it below, and we define only the minimal amount of logical material that is necessary to state and prove the theorem.

First-order logic

Consider the property “for every position that has label a, there is a later position that has label b”. This property can be formalized in the language of logic as

$\forall x a(x) \Rightarrow \exists y (x < y \land b(y))$

This is the idea behind first-order definable languages of words. One uses formulas, where the variables quantify over positions of the word, with a binary predicate $x < y$ that denotes the order on positions, and with unary predicates of the form $a(x)$ to test the labels of positions. A set of words is called first-order definable if there is a formula of this kind that is true on words from the set and false in other words. The term “first-order” refer to the fact that the logic can only quantify over single positions, as opposed to quantification over sets of positions, or sets of sets of positions, which would be possible in higher-order logics (e.g. monadic second-order logic mentioned above is allowed to quantify over sets of positions, but not sets of pairs of positions).

Example. The language $(a+b)^*b$ is definable in first-order logic, using the formula given above.

Star-free expressions.

Star-free expressions are, essentially, a minor variation on first-order logic. A star-free expression is a regular expression that does not use the star, but it can use complementation (with respect to an alphabet that is implicit in the expression). For example, if the input alphabet is $\Sigma$ , then the complement of the empty set is a star-free expression that describes $\Sigma^*$ . Using this expression, one can e.g. define the set of words that contain at least one letter $a$ , this is

$(\neg \emptyset) \cdot a \cdot (\neg \emptyset)$

Aperiodic monoids.

Call a finite monoid aperiodic if for every $m$ in the monoid, the sequence

$m,m^2,m^3,\ldots$

is ultimately constant. It is easy to see that this is equivalent to saying that every $m$ in the monoid satisfies

$m^\# =m^{\#}m$

where $m^\#$ is the idempotent power discussed here.

The Schützenberger theorem.

We are now ready to state the Schützenberger theorem.

Theorem. For a language $L \subseteq A^*$ , the following conditions are equivalent:

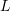$L$ is definable by a star-free expression;
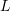$L$ is definable in first-order logic;
the syntactic monoid of 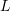$L$ is aperiodic.

Technically speaking, Schützenberger proved only the equivalence of 1 and 3, and the addition of 2 is due to McNaughton and Papert. The addition of 2 is not a big deal: the implication from 1 to 2 is done via a routine induction on the size of a star-free expression, while the implication from 2 to 3 is proved the same way as the implication from 1 to 3. Therefore, the theorem is essentially by Schützenberger.

As mentioned above, the implication from 1 to 2 is straightforward. The implication from 2 to 3 is proved here, while the implication from 3 to 1 is proved here.

COMMENTS

admin

October 31, 2017

Thanks Tobias! I hope that I have fixed the broken links now. Mikołaj

Tobias Heindel

October 23, 2017

http://duch.mimuw.edu.pl/~bojan/domowa/?page_id=126 gives a 404

zajęcia / courses

3. The Schützenberger Theorem

Leave a Reply