Zigzags

Mikołaj Bojańczyk

zajęcia / courses

Consider a set $X$ equipped with a well quasi-order $\le$ . For the application to piecewise testable languages, the set $X$ is the set of all words over a given finite alphabet, and $\le$ is the Higman ordering. Nevertheless, result presented here is true for well quasi-ordered sets in general, so we present it like that.

For two subsets $L,K \subseteq X$ , define an zigzag between $L$ and $K$ to be a sequence

$x_1 \le x_2 \le x_3 \le x_4 \le \cdots$

which alternates between $L$ and $K$ , i.e. if one element is in $L$ then the next one is in $K$ , and vice versa. Zigzags can be finite or infinite. If $L$ and $K$ have a common element $x$ , then there $x \le x \le x \le \dots$ is a zigzag of infinite length.

Zigzag Theorem. Let $L,K$ be subsets of a set $X$ equipped with a well quasi-order. Then the following conditions are equivalent

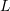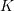the sets $L$ and $K$ can be separated by a finite Boolean combination of upward closed sets
there is no infinite zigzag between 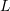$L$ and $K$
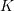
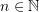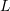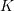there is some $n \in \mathbb N$ such that zigzags between $L$ and $K$ have length at most $n$

The rest of this page is devoted to proving the Zigzag Theorem.

1 implies 2. Suppose that $L$ and $K$ can be separated by a set $M$ which is a Boolean combination of upward closed sets

$M_1,\ldots,M_k$

As we progress along a zigzag, elements of the zigzag belong to more and more of the sets among $M_1,\ldots,M_k$ , and therefore all but finitely many elements of the zigzag must belong to the set $M$ , so it cannot be a separator.

2 implies 3. Consider the following graph, call it the zigzag graph: the vertices are elements of $L \cup K$ . There is an edge from every $x \in L$ to all elements in $x \uparrow \cap K$ , and likewise there is an edge from every $x \in K$ to all elements in $x \uparrow \cap L$ . A zigzag is the same thing as a path in the zigzag graph. Consider also the optimised zigzag graph, where the vertices are the same, but there are edges from $x \in L$ only to the minimal elements $x \uparrow \cap K$ , and likewise for $x \in K$ there are edges only to minimal elements of $x \uparrow \cap L$ . The point of the optimised zigzag graph is that it every vertex has finite degree (i.e. finitely many outgoing edges), because the outgoing edges yield an antichain, and antichains are finite.

It is not difficult to see that for every path in the zigzag graph, there is a path of same length in the optimised zigzag path (conversely, every path in the optimised zigzag graph is a path in the zigzag graph) . Therefore, to prove the implication from 2 to 3, it suffices to prove that if the optimised zigzag graph contains arbitrarily long paths, then it contains an infinite path. The optimised zigzag graph is actually a finite union of trees, whose roots correspond to minimal elements in $L \cup K$ , and therefore the König Lemma proves that if it contains arbitrarily long paths, then it contains an infinite path.

3 implies 1. Let us assume that zigzags between $L$ and $K$ have length at most $n$ . For $i \in \{1,\ldots,n\}$ , define

$L_1 \subseteq L_2 \subseteq \cdots \subseteq L_n = L$

so that $L_i$ is the set those elements of $L$ which admit zigzags of length at most $i$ . Here is a picture of these sets for $n=4$ , including a zigzag of length 4 that begins in $K$

Define $L_0$ and $K_0$ to be empty. By induction on $i \in \{0,\ldots,n\}$ , we prove that there exists a Boolean combination of upward closed sets $M_i$ which separates $L_i$ from $K \cup L - L_i$ . This is illustrated in the following picture for $n=4$ and $i=2$ .

The induction base is when $i=0$ , in which case $L_0$ is empty and therefore $M_0$ can also be empty.

Consider the induction step, i.e. assume that the property has been proved for $i$ now want to prove it for $i+1$ . Consider the upward closure of the set $K_{i+1}$ . We know that this upward closure is is disjoint with $L_{i+1}$ , Likewise, the upward closure of $L_{i+1}$ is disjoint with $K_i$ . This situation is shown in the following picture for $n=4$ and $i=2$ .

Therefore, $M_{i+1}$ can be defined to be the upward closure of $L_{i+1}$ minus the upward closure of $K_{i+1}$ and then finally plus $M_i$ .

zajęcia / courses

Zigzags

Leave a Reply