posts | Mikołaj Bojańczyk

Mikołaj Bojańczyk

On mustard watches

Fact. For every $n$ classical papers in a given field, there will be $O(n^2)$ mustard watch papers.

March 20, 2021

Slajdomat – my homegrown slide software

Slajdomat is a tool that I am developing for making zooming slides in Figma. You draw your slides in Figma, which is a good drawing program that can be used for free (you can also apply for an education plan which removes some limits of the free version), and is available on Mac, Windows, and as a web page. You use the Slajdomat plugin to annotate your picture with slide information (what is the slide order, and overlays). Then, you export the slides, with the result being html that you can upload to your website.

Design goals

uses Figma, which is a quality drawing program and free for basic use
zoom in and zoom out
allows recording sound
produces html, hopefully not bloated
has some math and latex support

How to install

Currently, there is a Mac version, but since the program is based on html and electron, versions for Windows and Linux should be available soon. (If you have windows, you can try to download the source, see below, and compile a windows version and send it to me.)

Download the software . Embarrassingly, this is 74MB. 99% is a copy of chrome, which is how electron works.
Open the downloaded zip. There are two parts: the Figma plugin, and the Slajdomat app. You can move the app to your applications directory. The app is responsible for creating the html files.
Install the figma plugin in Figma as follows. In Figma, select “Manage plugins” from the “Plugins” menu. When you are in the “Manage plugins” window, click the button “Create new plugin” from the “In development”. In the dialog for creating a new plugin, select “Click to choose a manifest.json file”, and choose the manifest.json file that is in the “figma-plugin” folder of Slajdomat. Eventually, when I have more confidence in the plugin, I will publish it to the Figma plugin collection, so this step will become simpler.

How to use

Drawing the slides in Figma. Once installed, the plugin is available in the “Plugins” menu. Each slide is Figma frame. Here is an overview of the interface:

There are two kinds of events: zoom events which correspond to switching slides, and show/hide events which change the current slide.

a zoom event, which zooms into a child slide. In the present slide, there is a corresponding red rectangle, which shows where the child slide will be placed. Keep the proportions of this rectangle unchanged – it should be the same proportions as the child – otherwise the zooming will have some distortion.
show and hide events, which concern the current slide (such events are called overlays events). A show event switches an object on the current slide (a picture, some text) from invisible to visible, a hide event does the opposite. If the first event for an object is show, then the object starts out invisible; if the first event is hide or there is no event, then the object starts out visible.

In the future, there might be new events, such as moving. The second black toolbar (with an eye and the “Overlays” and “Zoom” menus) is used to create new events. For the overlays events, you can create the event for several different objects at once. Also, overlays events can be grouped (by clicking a chain icon between the events), so that they execute at the same time. Likewise, zoom events can be grouped (in this case, you go directly from one child to another, without returning to the parent). One cannot group overlays with zoom events.

Saving the slides. So far, you have only used the Figma plugin. Now it is time for the app. Run the Slajdomat app, and select a folder where your slides will be stored. Now click the upload arrow in the top-left corner of the plugin. The plugin will connect to the Slajdomat app (via the internet, on port 3001, which can be changed in the settings) and send the slides. Upon receiving the slides, the Slajdomat app will create (or update, in case it already exists) a new folder with your slides. This folder will contain an index.html file, and therefore if you copy this folder to your website, then it will simply show the slides. You can also view your slides directly from the Slajdomat app.

Extra features

Sound. There is a – rather flaky – feature to add sound to your slides. When you are in the Slajdomat app, you can click on your slides and view them. When you press the “r” key, it will start recording sound. You then start talking, and press the right arrow whenever you want to continue to the next slide. Recording stops once you press “r”, space, or left arrow. You can re-record the sound for parts of the presentation.

Drawing. While playing a presentation, you can press “d” which will display a very rudimentary drawing tool (pencils in two colours, and undo).

Math. The plugin also has some features for math. There is a button that runs latex (using a web service called web-cogs), importantly there is also de-latex, which means you can keep on correcting your formulas. Also, there is a feature for inserting a special character in a configurable math font. For example, I write most of my text using a font that has poor math symbols, and I use a font like FDSymbol for math symbols.

Source code and contributing

You can find the source code on GitHub. This is a good place for sending bug reports and feature requests. If you might want to joint the project, let me know, although I admit I have no experience in managing a software project.

August 19, 2020

Citations not correlated with referee scores

I logged into my easychair account, and downloaded the average referee scores for 184 accepted papers. These are taken from conferences (ICALP, STACS and LICS) where I was in the PC, so I had access to the scores for the papers. In all cases, the scores were on a scale of -3 to +3, so they can be compared. Next, for each paper I looked at the number citations, according to google scholar. Here is the result (y axis is citations and x axis is average referee score):

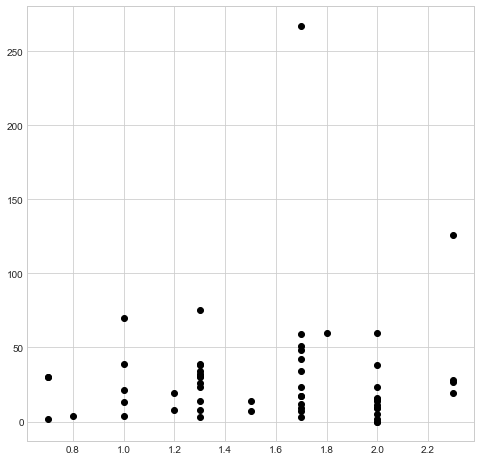
You will see that there does not seem to be any strong relationship between the two variables. In fact, the correlation is negative (-0.004539).

I understand that citation counts are a questionable metric, whose main advantage is that it can be counted and drawn in a scatter plot. Nevertheless, I think that these results are evidence for the fact that reviews, especially for conferences, do not reflect the value of the paper. My personal impression is that for conferences, higher scores are given for papers of the kind “we continue the work of x by solving problem y” and lower scores are given for papers of the kind “we introduce a new idea”. On the other hand, the impact (and therefore also citations) is greater for the second kind.

Of course I do not recommend to get rid of reviews, since there does not seem to be any better system.

December 11, 2019

How to improve your citations with one simple trick

The trick. You cannot write “as shown in [3]”, but you need to write “as shown in [3, Theorem 2]” or “as shown in [3, p. 122]”.

Analysis. This does not take too much work. When first citing a result/definition, you need to invest 5 minutes to download the paper and then search for “Theorem” or “Main Theorem”. Advantages of this system:

Sometimes, the theorem does not say what you wanted, because it has an unfortunate extra assumption. An often repeated comment is that it is hard to parse the cryptic language of old papers, but I think that: (a) old papers are often not so cryptic; (b) if they are, then just can suck it up – you want to avoid a common source of mistakes which is an incorrect identification of two definitions; (c) maybe the different formalism in the old paper is there for a good reason.
Sometimes, you will find a footnote next to the Main Theorem, which says that “this theorem was already proved before by x”. This can happen even for the most central results from your field, which have been cited countless times, apparently without anybody every opening the paper. It reminds me of the time when I went to my school library to find out what’s so great about Żeromski, but found that the pages were un-cut in his books that were not compulsory reading.
You will avoid the scourge of “this topic was also studied in [1,5,10,12,13]” and other silly citations. What is “the topic” and how was it “studied”?

December 7, 2019

Who to cite: MSO transductions

This page is intended as notes, mainly for myself, about the history of some notions in logic and automata. But maybe they can be useful to others. These notes will surely have many wrong statements, so I welcome comments and corrections.

MSO transductions

An mso transduction is a transformation which inputs a structure (a word, tree, graph, etc.) and outputs another structure. My conclusion is that mso transductions can be credited to the following papers:

An ICALP paper by Arnborg, Lagergren and Seese called Problems easy for tree-decomposable graphs (1988). The journal version appeared in 1991.
The journal version of Courcelle’s The monadic second-order logic of graphs V (1991). The technical report appeared in 1989.
A workshop paper by Engelfriet called A characterization of context-free NCE graph languages by monadic second-order logic on trees (1991) The paper cites slides of Engelfriet from 1988.

If, for reasons of brevity, one wishes to cite just a single paper, while still using a source close to the originals, then one can use:

the survey Monadic second-order definable graph transductions: a survey (1994) by Courcelle
the book Graph Structure and Monadic Second-Order Logic – A Language-Theoretic Approach (2012) by Courcelle and Engelfriet

A longer discussion is given below. In his survey article from 1994, Courcelle tells the following story:

Paper [1] is the Arnborg et al. paper from 1988. Paper [22] is the 1991 paper of Engelfriet from 1991. Papers [9,10,13] are items VI, V, VII of Courcelle’s series The monadic second-order logic of graphs, published in 1990 and 1991. Finally [15] is a joint research report of Courcelle and Engelfriet.

Papers [1,22,9] are discussed below.

We begin with Arnborg et al., which has the earliest date. In Problems easy for tree-decomposable graphs (1988), by Arnborg, Lagergren and Seese, the authors introduce a version of mso transductions and place it in context as follows:

Here is their definition:

It is worth pointing out that this definition is a function, i.e. it does not have nondeterministic colouring. Also, it allows quotienting, thanks to ε, which is a feature commonly used for first-order interpretations, but which has not caught on for mso transductions. Maybe it has not caught on since the existentially guessed colouring, which will appear in Courcelle’s definition, eliminates the need for quotienting.

We now move on to the Engelfriet paper, A characterization of context-free NCE graph languages by monadic second-order logic on trees (1991). Englefriet gives the following story of mso transductions, which is the same as Courcelle’s:

Enelfriet’s definition is this:

Also here, there is no nondeterministic colouring. The definition is for the vocabulary of graphs, but of course any reasonable person can apply it to other structures. The above definition does not allow quotienting, but it does allow defining partial functions, thanks to the domain formula.

Finally, let’s look at Courcelle’s The monadic second-order logic of graphs V from 1991. Here we find the following definition of mso transductions:

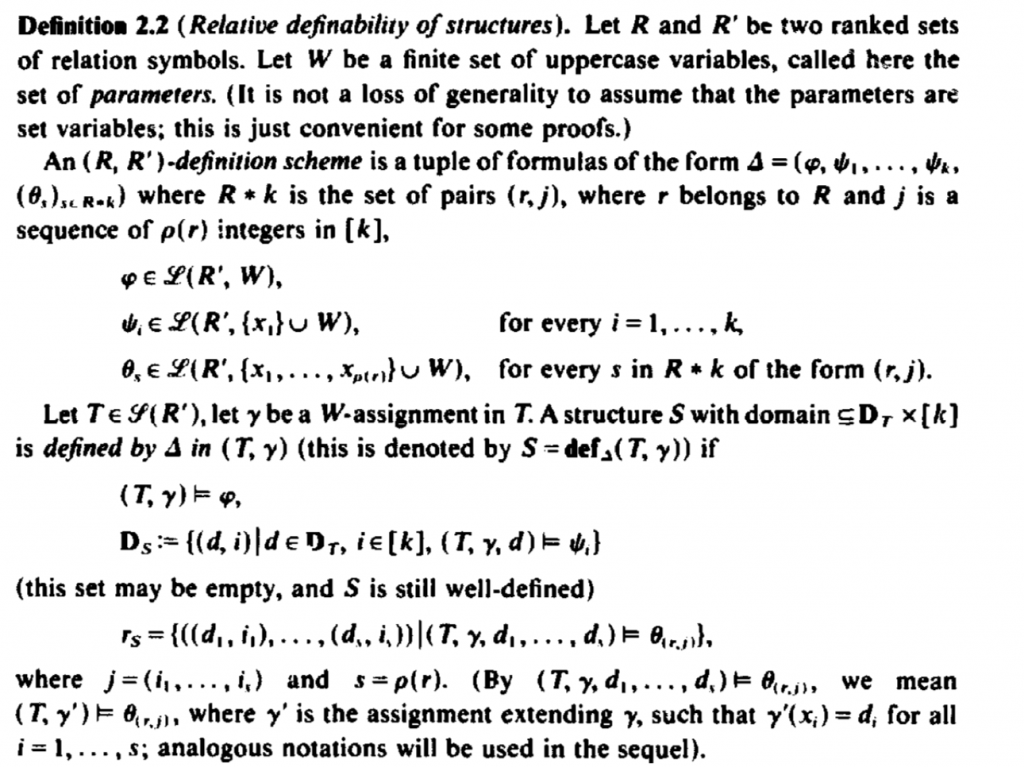
The eagle-eyed reader will notice two features that were not present in the previous definitions: copying (this is the number k) and an existentially quantified colouring of the input structure (this is W). Copying is maybe not such a big deal, but the colouring is important. For example, in the same paper Courcelle states his conjecture:

The solution of this conjecture crucially relies on the colouring. For linearly ordered input structures, such as trees or words, the colouring is less important, since the lexicographically least colouring that works can be computed by a formula.

May 31, 2019

PhD Open Lecture Problems

You can get points by either finding mistakes in the atom book or by solving problems.

Grades:3=2 points, 4=2.5 points, 5=3 points.

Deadline: June 30

Mistakes

Each mistake in the atom book (not counting solutions to exercises) gets you 0.1 points. Mark the mistakes on this page with your name, if it does not work you can use this google docs. Mistakes also include typos, bad grammar, and unclear parts (explain why), generally speaking anything that requires improvement. You don’t need to start to read the book from the beginning. The lecture corresponds to Chapters 3,4,7 and 10, but you are encouraged to find mistakes in other parts (later chapters have a higher expected mistake rate, so it might be profitable to look at them).

Problems

Each of the problems (see below) gets you 1 point if it is solved by ≥3 people including you, 2 points otherwise.

Define a register automaton to be an equivariant automaton where the state space is of the form
$\atoms^{k_1} + \cdots + \atoms^{k_n}$

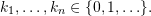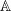for some $k_1,\ldots,k_n \in \set{0,1,\ldots}.$ Find an example of oligomorphic atoms $\atoms$ and a language over input alphabet $\atoms$ which is recognised by a deterministic orbit-finite automaton, but is not recognised by any equivariant deterministic register automaton.
Show an example of infinite oligomorphic atoms which satisfy the following property (*): if a language 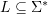$L \subseteq \Sigma^*$ is recognised by (hereditarily orbit-finite) deterministic Turing machine, then the same is true for
$\set{w : aw \in L \text{ for some } a \in \Sigma}.$
Show an example of infinite oligomorphic atoms where the property (*) from the previous problem is false.
Assume that the atoms are the random undirected graph. Are the following two conditions equivalent for a class 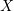$X$ of finite graphs? (a) There is an equivariant nondeterministic orbit-finite automaton with input alphabet 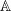$\atoms$ which recognises the language

${\color{red}\set{a_1 \cdots a_n : \text{$n \in \Nat$ and the subgraph of $\atoms$ induced by $\set{a_1,\ldots,a_n}$ belongs to $X$}}}$

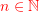(b) there is some ${\color{red} n \in \Nat}$ such that property 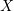$X$ can be defined by a formula of first-order logic which has shape

$\exists x_1 \exists x_2 \cdots \exists x_n \forall y \underbrace{\varphi(x_1,x_2,\ldots,x_n,y)}_{\substack{\text{quantifier-free using} \\ \text{only the edge relation}}}$
Assume that the atoms are the universal tree, i.e. the limit of trees modelled as structures with a closest common ancestor function. Is there are set builder expression, without constants, which defines a dense total order $(X,<)$ ?
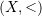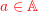Let $\color{red} \atoms$ be oligomorphic atoms. Show that for every $\color{red} a \in \atoms$ there can only be finitely many atoms $\color{red} b \in \atoms$ such that the $\color{red} a$ -orbit of $\color{red} b$ is finite.
Let $\color{red} \atoms$ be infinite oligomorphic atoms. Show that deterministic orbit-finite automata recognise strictly more languages than orbit-finite monoids.
Let $\color{red} \atoms$ be infinite oligomorphic atoms. Show that universality is undecidable for nondeterministic orbit-finite automata.
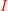Consider the equality atoms. We say that a class of languages $\color{red} \mathcal L$ is closed under orbit-finite union if for every orbit-finite set $\color{red} I$ and finitely supported function $\color{red} f : I \to \mathcal L$ , the class also contains the union
$\color{red} \bigcup_{i \in I} f(i).$

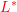Define the regular expressions to be the smallest class of languages (over orbit-finite alphabets) which: contains all languages with finitely many words and is closed under orbit-finite union, concatenation $\color{red} L \cdot K$ and Kleene star $\color{red} L^*$ . Do regular expressions define the same languages as nondeterministic-orbit finite automata?

March 30, 2018

Lipa Summer School 2018 (June 25-28)

The Lipa Summer School (click here for the page of the school, including registration) is a summer school on topics connected to logic in computer science. The school consists of 4 mini-courses given by:

Rajeev Alur (UPenn) Regular processing of data streams
Matt Valeriote (McMaster) Finite algebras and connections with tree languages
Igor Walukiewicz (Bordeaux) MSOL and higher-order computation
Mikołaj Bojańczyk (Warsaw, organiser) Recognisable languages of graphs

January 31, 2018

How to run my slides

My slides are now deemed a security risk. To run them in Chrome, click this button:

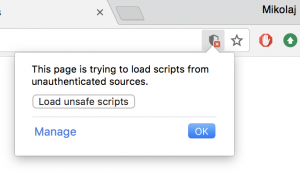
I promise I’m not trying to hurt your computer. Promise.

I will be working on a better solution.

October 2, 2017

Hilbert’s Basis Theorem and transducers

These slides show how to decide equivalence of tree-to-string transducers using the Hilbert Basis Theorem. The idea is based on

Helmut Seidl, Sebastian Maneth, Gregor Kemper:
Equivalence of Deterministic Top-Down Tree-to-String Transducers is Decidable. FOCS 2015: 943-962

There are two parts:

consider grammars that generate tuples of rational numbers, and use the Hilbert Basis Theorem to show that the following is decidable: “given a grammar, decide if the only tuple that it generates is the zero tuple”. slides
reduce the equivalence problem for transducers to the zero-ness problem discussed above. slides

May 8, 2017

Lipa Summer School (July 3-6, 2017)

The Lipa Summer School (click here for the page of the school, including registration) is a summer school on topics connected to logic in computer science. There will be 4 mini-courses given by:

Stephan Kreutzer (Berlin) Algorithmic meta-theorems
Joël Ouaknine (Saarbrücken) Decision Problems for Linear Recurrence Sequences
Moshe Vardi (Rice) Linear-time verification and synthesis
Mikołaj Bojańczyk (Warsaw, organiser) What is a recognisable language?

March 27, 2017

Positions (deadline April 30, 2017)

I am leading an ERC Consolidator grant on automata and logic called “A unified theory of finite-state recognisability”. The main goal is to find algebraic structures (like monoids) for things like infinite trees or profinite words. However, I can be very flexible on the topic, as long as it is tangentially connected to logic or automata.

I am searching for talented postdocs and phd students. The deadline for applications is April 30, 2017. Send applications to me by email. Please feel to ask questions before that date!

Postdocs. The postdoc can begin at any time from June 1 until the end of 2017. The duration is 6 – 12 months, with a possibility of extension for another year. The application consists of your name and 1-2 names of people who can provide references. I am looking for people with a good track record in the top conferences of the field. Teaching is optional.

PhD students. A typical duration is 4 years, starting any time from June 1 until the end of 2017. In application please include a cv and 1-2 names of people who can provide references. I am looking for candidates with a strong background in mathematics.

August 13, 2016

Quiz

Take this quiz on formal language theory.

August 17, 2015

Complexity tables – a personal perspective

August 11, 2015

Tree width à la metro

Here is a way of drawing graphs of bounded tree width, inspired by metro maps. The horizontal black lines are graph edges, the coloured shapes are vertices, and the gray background is the tree underlying the decomposition.

The mathematical content of the picture is that a graph has tree width k if and only if it is a subgraph of a (k+1)-colourable chordal graph (thanks to Michał Pilipczuk for pointing this out).

June 20, 2015

EATCS council

In 2013, I joined the EATCS council. Here is what I promised to do:

I am a candidate for the EATCS council. My program consists of three items. The first item is something where I promise concrete action, the remaining two are more speculative.

I will support open access, in particular for ICALP proceedings.
In the long term, I think that the TCS community should move from publishing in conferences to publishing in journals. The ensuing travel is a waste of time and money. It is not clear to me how the EATCS can help solve this problem right now, without losing the accumulated prestige capital of ICALP. Maybe ICALP could move to a continuous submission model like VLDB?
It is my impression that the current EATCS members are mainly people who have recently attended ICALP, which is a bit random. Membership should be made more representative. Maybe we should make membership free (but still feed EATCS from an ICALP tax)?

Update. The first item is solved: starting with 2016, ICALP will be using the open access LIPICS system. As it turned out, this idea had overwhelming support inside the council.

June 20, 2015

Mojżesz Presburger in Warsaw

A presentation on documents about Mojżesz Presburger from the archives of Warsaw University

The documents in high resolution:

Birth certificate (Presburger was born in 1904, but this document is from August 1923)

Matura (May 1923) (Very big)

Application to study at Warsaw University (September 1923)

Hand-written CV (September 1923)

Student ID card

Courses for the winter semester in 1924

Courses for the autumn/winter trimester in 1927/28

Graduation diploma (October 1930) (1/2)

Graduation diploma (October 1930) (2/2)

Court document concerning 70 złoty unpaid tuition (January 1939)