This page is intended as notes, mainly for myself, about the history of some notions in logic and automata. But maybe they can be useful to others. These notes will surely have many wrong statements, so I welcome comments and corrections.

MSO transductions

An mso transduction is a transformation which inputs a structure (a word, tree, graph, etc.) and outputs another structure. My conclusion is that mso transductions can be credited to the following papers:

• An ICALP paper by  Arnborg, Lagergren and Seese called Problems easy for tree-decomposable graphs (1988). The journal version appeared in 1991.
• The journal version of Courcelle’s The monadic second-order logic of graphs V (1991). The technical report appeared in 1989.
• A workshop paper by Engelfriet called  A characterization of context-free NCE graph languages by monadic second-order logic on trees (1991) The paper cites slides of Engelfriet from 1988.

If, for reasons of brevity, one wishes to cite just a single paper, while still using a source close to the originals, then one can use:

•  the survey Monadic second-order definable graph transductions: a survey (1994) by Courcelle
• the book Graph Structure and Monadic Second-Order Logic – A Language-Theoretic Approach (2012) by Courcelle and Engelfriet

A longer discussion is given below.  In his survey article from 1994, Courcelle tells the following story:

Paper [1] is the Arnborg et al. paper from 1988. Paper [22] is the 1991 paper of  Engelfriet from 1991. Papers [9,10,13] are items VI, V, VII of Courcelle’s series The monadic second-order logic of graphs, published in 1990 and 1991. Finally [15] is a joint research report of Courcelle and Engelfriet.

Papers [1,22,9] are discussed below.

We begin with Arnborg et al., which has the earliest date. In Problems easy for tree-decomposable graphs (1988), by  Arnborg, Lagergren and Seese, the authors introduce a version of  mso transductions and place it in context as follows:

Here is their definition:

It is worth pointing out that this definition is a function, i.e. it does not have nondeterministic colouring. Also, it allows quotienting, thanks to ε, which is a feature commonly used for first-order interpretations, but which has not caught on for mso transductions. Maybe it has not caught on since the existentially guessed colouring, which will appear in Courcelle’s definition, eliminates the need for quotienting.

We now move on to the Engelfriet paper, A characterization of context-free NCE graph languages by monadic second-order logic on trees (1991).  Englefriet gives the following story of mso transductions, which is the same as Courcelle’s:

Enelfriet’s definition is this:

Also here, there is no nondeterministic colouring. The definition is for the vocabulary of graphs, but of course any reasonable person can apply it to other structures. The above definition does not allow quotienting, but it does allow defining partial functions, thanks to the domain formula.

Finally, let’s look at Courcelle’s The monadic second-order logic of graphs V from 1991. Here we find the following definition of mso transductions:

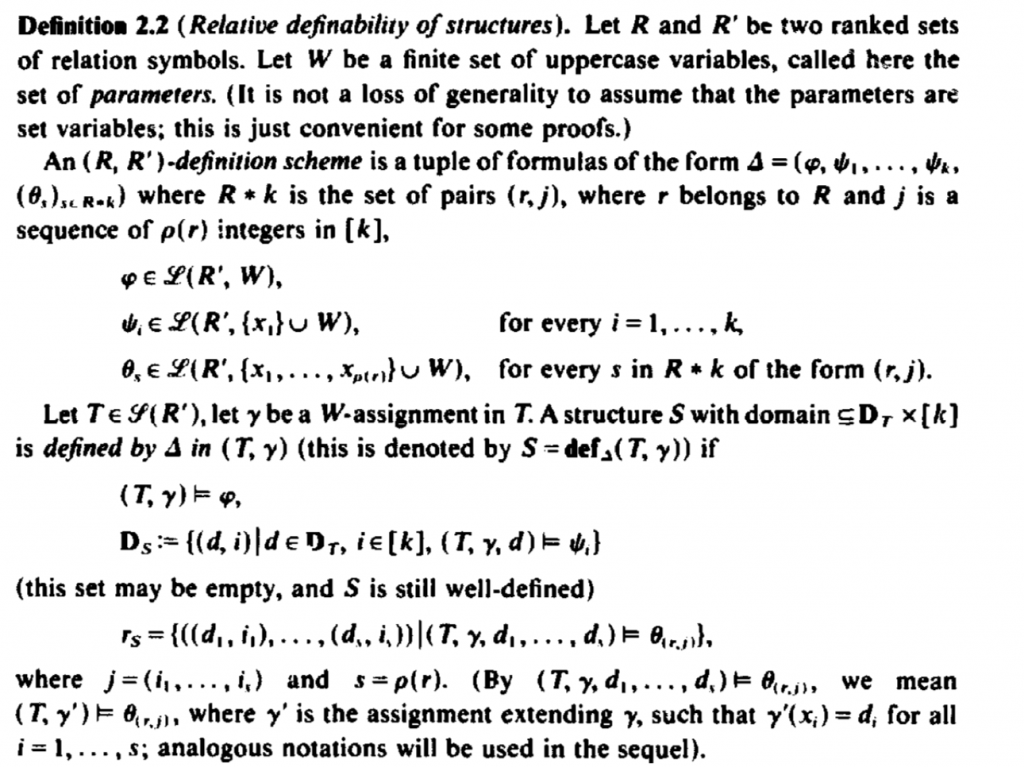
The eagle-eyed reader will notice two features that were not present in the previous definitions: copying (this is the number k) and an existentially quantified colouring of the input structure (this is W). Copying is maybe not such a big deal, but the colouring is important. For example, in the same paper Courcelle states his conjecture:

The solution of this conjecture crucially relies on the colouring. For linearly ordered input structures, such as trees or words, the colouring is less important, since the lexicographically least colouring that works can be computed by a formula.

 

COMMENTS