...czyli jak uzywac Maple V do rozwiazywania i wizualizacji prostych rownan rozniczkowych zwyczajnych.
Mozna (oczywiscie) to rownanie rozwiazac analitycznie, dostajac
x(t) = C exp(t).
Maple V tez to potrafi. Potrafi tez duzo wiecej. Aby szukac rozwiazania analitycznego, musimy najpierw zdefiniowac rownanie, ktore bedziemy rozwiazywac. Powiedzmy, ze bedzie sie ono nazywac `eq`:
> eq := diff( x(t), t ) = x(t);
(w podreczniku to rownanie nazwalibysmy zapewne nie `eq`, ale `(*)`).
Po zdefiniowaniu rownania, mozemy je od razu sprobowac rozwiazac:
> dsolve( eq, x(t) );
x(t) = _C1 exp(t)
Rownanie jest na tyle proste, ze oczywiscie udaje sie nam dostac analityczne rozwiazanie. Zauwazmy od razu, ze Maple V automatycznie dodaje potrzebne stale - nie podalismy przeciez zadnych warunkow poczatkowych!
Aby wyznaczyc rozwiazanie naszego rownania z warunkiem poczatkowym, np. x(0) = 1, wystarczy podac te informacje w pierwszym argumencie dsolve():
> dsolve( {eq, x(0) = 1}, x(t) );
Nastepnie mozna juz obejrzec rozwiazanie
> plot( rhs("), t = -1..1 );
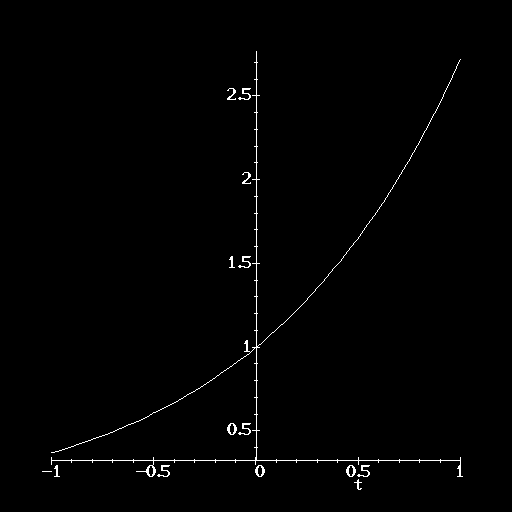
Tajemniczo wygladajaca sekwencja rhs(") tlumaczy sie nastepujaco: " oznacza wynik ostatniego obliczenia Maple V. U nas jest to oczywiscie rownosc x(t) = exp(t). Z kolei rhs() zwraca prawa strone rownosci (ang. right hand side), czyli u nas exp(t) - i wlasnie to wyrazenie podstawia sie jako pierwszy argument (tzn. 'co narysowac?') funkcji plot()
Jak wiec widac, standardowa sciezka postepowania przy rozwiazywaniu rownan zwyczajnych w Maple V jest nastepujaca:
Rozwiazac przy uzyciu dsolve().
Obejrzec wykres.
Nietrudno zgadnac, ze czesto standardowa sciezka nie wystarczy...