Here are 4 difficult exercises. If an exercise is solved by  people, then each solver gets  points, which are added to the grade. Grades are rounded to the closest number from the set {2, 3, 3.5, 4, 4.5, 5}. For example, if in the oral exam you got a 4, and you were the only person to solve one exercise, then you get 4.7 points, which is rounded to 4.5. The deadline is January 15, 2018.

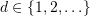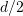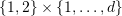1.  Let  . Show that there is no deterministic reachability automaton with less than states which accepts every -word over alphabet where all loops are even (in the sense Lemma 3.2 in the notes), and rejects every -word where all loops are odd.  (If you can give a better lower bound, like 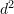, even for 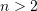, then we will be glad to hear – you can contact Wojciech Czerwiński who is working on this problem.)
2. Show that the following problem is decidable. The input is a vector addition system, of dimension say 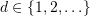, and a source configuration 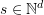. The question: is it the case that for every 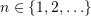there exists a run that begins in configuration and ends in a configuration ?
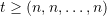3. Consider a nondeterministic tree automaton (as defined in Definition 5.1 in the notes). Call it unambiguous if for every input tree it has at most one accepting run. Show that equivalence (i.e. accepting the same trees) of unambiguous tree automata can be decided in polynomial time.
4. Prove or disprove (we do not know the answer): every tree language recognised by a deterministic top-down tree automaton (see Definition 5.1 in the notes) is also recognised by a deterministic tree-walking automaton.