Tree width

Mikołaj Bojańczyk

zajęcia / courses

In this page, we define tree decompositions and treewidth. We will define tree decompositions in two ways: less and more algebraically. The less algebraic way is more common in the literature, so we begin with that. The more algebraic way will be more convenient for our presentation of the Courcelle theorem, and is given later.

Tree width

Consider an undirected graph $G$ . Define a tree decomposition of $G$ to be a tree $t$ together with a labelling

$v \in \text{nodes of $t$} \qquad \mapsto \qquad \text{bag of $v$ $\subseteq $ vertices of $G$}$

such that the following properties hold:

every edge of 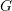$G$ is contained in bag of $t$ ;
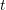for every vertex in 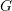$G$ , the set of nodes in 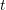$t$ whose bags contain $v$ is connected via the child relation.

As an example, consider the following graph:

Here is a tree decomposition of the above graph:

In the above picture, the nodes are the blue circles, and the subgraphs induced by the bags are drawn inside the nodes. Define the width of a tree decomposition to be the maximal size of a bag minus one. In the example above, the width is 2, because the maximal bag size is 3. (If you don’t like doing minus one, an alternative view is that the width is the maximal intersection of two bags of adjacent nodes.) The tree width of a graph is the minimal width of a tree decomposition of it.

Sourced graphs: an algebraic view of treewidth

We now present a more algebraic way of defining treewidth. Define a sourced graph to be a graph with some but not necessarily all vertices being assigned natural numbers; the vertices with numbers are called the sources. The numbers are called the source names. We assume that the each source has one number; although the numbers used in a graph need not be a prefix of $\set{0,1,\ldots}$ . A sourced graph with no sources is the same thing as a graph. Here is a picture of a sourced graph, with the source names used being $\set{1,2,4}$ :

The main purpose of sourced graphs is to fuse them using a fusion operation $\oplus$ . The operation inputs two sourced graphs. On the output, it produces the disjoint union of the two inputs, with each pair of sources that have the same name being merged together into a single vertex (when we merged vertices $v$ and $w$ , all edges incident with $v$ and $w$ are redirected to the new merged vertex). The fusion operation can easily be extended to take not two arguments, but any number of arguments in $\set{1,2,\ldots}$ . When there is one argument, nothing happens.

After doing a fusion, we might want to forget some source names. For this we use an extended forgetting version of the fusion operation $\oplus_X$ , where the index is a set $X$ source names, i.e. natural numbers. When this operation is applied, we first do the fusion as described above, and then we only keep the source names from $X$ , while sources with names outside $X$ become non-sources. Let us illustrate the forgetting fusion operation on an example. Consider the following two sourced graphs:

Note that the two sourced graphs above share common source names, namely 2 and 4, while the source names 1 and 3 are not common. Therefore, when fusing them we will do two merges: one for source name 2, and one for source name 4. Suppose that the two sourced graphs above are combined using the operation $\oplus_{\set{2,3}}$ . The result will be the following interface graph.

The colours blue, yellow and green are supposed to indicate which of the inputs was used to produce which vertex, and they are not part of the actual sourced graph.

Algebra of sourced graphs. The set of sourced graphs can be viewed as an algebra, which we call the algebra of sourced graphs. This algebra has a constant for every sourced graph, and a binary operation $\oplus_X$ for every finite set $X$ of source names. Here is an example of a term in the algebra of sourced graphs which generates a cycle of length 6:

Theorem. A graph has treewidth $k$ if and only if it (when viewed as a sourced graph without any sources) can be generated by a term in the algebra of sourced graphs, using only constants that have at most $k+1$ vertices and source names in $\set{1,\ldots,k+1}$ .

Proof. We only sketch the slightly more interesting top-down implication. Consider a tree decomposition (in the standard, non-algebraic way). We assume that it is rooted, so that we can speak about the subtree of a node. For node $x$ , define its cone to be the sourced graph which consists of the union of the bags in $x$ and its descendant, and where the sources are those vertices that appear both in $x$ and in the parent of $x$ . Here is a picture:

By induction on the number of descendants of $x$ , we show that the cone of $x$ can be generated by a term in the algebra of sourced graphs, with resources bounded as in the theorem (i.e. constants use at most $k+1$ vertices and source names from $\set{1,\ldots,k+1}$ ). More precisely, for any labelling of the sources in the cone by numbers in $\set{1,\ldots,k+1}$ , we can create an appropriate term. Here is a picture of the induction step: