In this page we prove Theorem 1 below, which says that tree decompositions of slightly suboptimal width can be computed in cubic time. More precisely, we show that for every there is a cubic time algorithm which inputs a graph and fails or outputs a tree decomposition of width . The algorithm succeeds if the input graph has tree width . The constants in the cubic time depend exponentially on .  The theorem includes a set of distinguished vertices, which are used in its proof, but for external purposes like Courcelle’s Theorem one can assume that the set of distinguished vertices is empty.

Theorem 1. Fix . There is a cubic time algorithm which does this:

• Input: A graph with at most 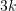distinguished vertices;
• Output: Failure, or a tree decomposition of the graph which has width 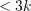  and has all distinguished vertices in the root bag.

If the input graph has treewidth   then the algorithm succeeds.

The result mentioned at the beginning is the special case of Theorem 1 when there are no distinguished vertices. The constant in the running time of the algorithm is exponential in . Theorem 1 is not the optimal result. One can improve it in two ways: a) the running time can be made linear; and b) the tree decompositions computed can have optimal width. The two improvements can be done together. For Courcelle’s Theorem, we do not need optimal width tree decompositions, so improvement b) would not change anything. On the other hand, improvement a) would make the running time in Courcelle’s Theorem linear. Since both improvements a) and b) require substantial technical work, we present Theorem 1 in its present, suboptimal form, since that can be rather easily shown.

The rest of this page is devoted to proving Theorem 1. In the algorithm, we use the following result on computing separators.

Theorem 2. Given a graph and disjoint sets of vertices , one can compute in quadratic time (in the number of edges) a separator of minimal size. Recall that a separator is a set of vertices disjoint from such that does not contain any path connecting with .

We do not prove the above theorem, it can be shown using the Ford-Fulkerson algorithm. Actually, more fancy algorithms have subquadratic running time. The main step in proving Theorem 1 is the following lemma.

Lemma. Let . There is a quadratic time algorithm, which does this:

• Input: A graph with a set 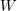of at most 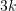distinguished vertices.
• Output: Failure, or a set 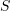of at most 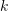vertices in the graph, and a partition of 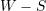into two parts 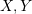, each part of size at most 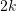and such that 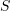separates the two parts. 

If the input graph has treewidth   then the algorithm succeeds.

Proof of the lemma. We begin with the algorithm, and only later we justify why it must succeed on graphs of treewidth . Let the input graph be . We enumerate all possible partitions of into three parts , such that has size at most , and each of has size at most . The idea is that is the intersection . The number of such partitions is exponential in , but is a constant if is assumed to be fixed. For each such partition, we compute a minimal size separator of and in the graph , and we report success if the combined size of and is at most . This completes the algorithm.

We now justify that if has treewidth then the algorithm succeeds. If the graph has treewidth , then there is a tree decomposition where all bags have size at most . Let be this tree decomposition. Choose a node of the tree decomposition so that at least half of the distinguished vertices of appear in bags of and its descendants, but this is no longer true for any of the children of . Define to be the bag of , the size of is at most . Furthermore, by choice of we know that every connected component of has at most half the distinguished vertices.

It remains to show that can be partitioned into two parts, call them and , such that separates them, and each part has size at most . To do this suppose that has connected components, and for define to be the distinguished vertices in the -th connected component of . Since each has at most half of the distinguished vertices, it follows that there must be some such that both of the sets

   

have at most two thirds of the distinguished vertices, i.e. at most distinguished vertices.

 

Proof of Theorem 1. Suppose that is a graph and is a set of at most distinguished vertices. If there are less than distinguished vertices, we add some arbitrary vertices to make the set have size exactly . Apply the lemma, computing and . If the input graph has treewidth then the algorithm from the lemma must succeed. Find all connected components of the graph . We know that each connected component has at most distinguished vertices. For each set of vertices which is a connected component of the graph , recursively call the algorithm for the subgraph of induced by , with the distinguished vertices being ; let be the resulting tree decomposition. Note that we are allowed to do the recursive call, since has at most vertices and has at most vertices, and thus there are at most distinguished vertices. The tree decomposition for the entire graph looks like this. The root bag consists of the distinguished vertices . For each connected component in , we add the tree decomposition as a child of the root. It is not difficult to check that this is a tree decomposition of . The algorithm does a quadratic computation, followed by recursive calls to smaller instances; and therefore its running time is cubic.