Mso and automata on finite trees

Mikołaj Bojańczyk

zajęcia / courses

Finite trees and their automata.

Apart from graphs, we will also use mso to define properties of trees (and their special case, words). Define a ranked alphabet to be a finite set $\Sigma$ where every element $a \in \Sigma$ has an associated arity in $\set{0,1,\ldots}$ . Here is a picture of a ranked alphabet:

A tree over a ranked alphabet $\Sigma$ is defined to be a (rooted) tree where every node has a label from $\Sigma$ . Furthermore, for each node the number of children is the same as the rank of the label, and we assume that these children are ordered, i.e. one can speak of the first child, second child, etc. Here is a picture of a tree over the alphabet from the example above:

A tree $t$ over an alphabet $\Sigma$ can be viewed as a logical structure, call it $\underline t$ . The universe of $\underline t$ is the nodes. For every $i \in \set{0,1,\ldots}$ there is a binary predicate $child_i(x,y)$ which says that $y$ is the $i$ -th child of $x$ , and for every $a \in \Sigma$ there is a predicate $a(x)$ which says that $x$ has label $a$ . Using mso, one can define a descendant predicate: a node $y$ is a descendant of $x$ if and only if every $y$ belongs to every set $X$ that contains $x$ and is closed under children.

We say that a set of trees $L$ over a ranked alphabet $\Sigma$ is mso definable if there is an mso formula $\varphi$ such that

$\underline t \models \varphi \quad \mbox{iff} \quad t \in L \qquad \mbox{for every tree $t$ over $\Sigma$}$

Examples of mso definable sets of trees include: “the number of nodes is divisible by 3” or “some root-to-leaf path has even length”.

Tree automata

Apart from mso, another mechanism of defining sets of trees (also known as tree languages) is to use automata. There also exist regular expressions for trees, but we do not discuss those here.

A (nondeterministic) tree automaton consists of:

an input alphabet 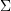$\Sigma$ , which is a ranked alphabet
a finite set of states 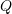$Q$ with a distinguished accepting subset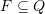 $F \subseteq Q$
for every letter 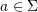$a \in \Sigma$ of rank $n$ , a transition relation 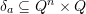$\delta_a \subseteq Q^n \times Q$ .

An automaton is called deterministic if every transition relation is actually a function $Q^n \to Q$ . A run of the automaton over an input tree $t$ is a labelling of tree nodes by states which is consistent with the transition relation in the following sense: if a node $x$ has label $a$ and its children have states $q_1,\ldots,q_n$ then the state in node $x$ satisfies

$(q_1,\ldots,q_n,q) \in \delta_a.$

Note that that this definition covers the special case of leaves; if a leaf has label $a$ then the transition relation $\delta_a \subseteq Q$ indicates what are the states allowed in leaves with state $a$ . Therefore, the transition relations for labels of rank zero can be viewed as initial states in the automaton. A tree is accepted by the automaton if there is some run which has an accepting state in the root. Therefore, one can view the run of the automaton as a bottom-up pass through the tree, which is considered accepting if the last state (the root) has an accepting state. That is why the automaton model described above is sometimes called a bottom-up automaton; although the distinction between top-down or bottom-up makes most sense when talking about deterministic automata.

The same proof as for automata on words, i.e. the subset construction, shows that tree automata can be determinised. The proof of the following theorem is skipped, it is a straightforward induction on the size of an mso formula. The proof uses the fact that tree automata have all the closure properties that correspond to operators in mso formulas, such as Boolean combinations and projections (guessing).

Theorem. If a tree language $L \subseteq \mathsf{trees}\Sigma$ is definable in mso, then it is recognised by some tree automaton.

The converse of the above theorem is also true, i.e. every language definable by a tree automaton can be defined in mso.

zajęcia / courses

Mso and automata on finite trees

Mso and automata on finite trees

Leave a Reply