 |
Refinement verification is methodology of verifying that the functionality of an abstract system model is correctly implemented by a low-level implementation. It can be used, for example, to verify that a packet router or bus protocol, modeled at the clock-cycle level, correctly implements a given abstract model of end-to-end data transfer. Similarly one can verify that a clock-accurate model of a pipelined, out-of-order processor correctly implements a given instruct-set architecture (i.e., a programmer's model of a machine).
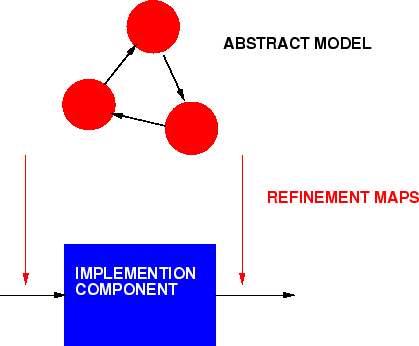
By breaking a large verification problem into small, manageable parts, the refinement methodology makes it possible to verify designs that are much too large to be handled directly by model checking. This decomposition of the verification problem is enabled by specifying refinement maps that translate the behavior of the abstract model into the behavior of given interfaces and structures in the low-level design. This makes it possible to verify small parts of the low-level design in the context of the abstract model. Thus, the proof obligations can be reduced to a small enough scale to be verified by model checking.
SMV supports this methodology by allowing one to specify many abstract definitions for the same signal. A new construct called a ``layer'' is introduced for this purpose. A layer is a collection of abstract signal definitions. A layer can, for example, define low-level implementation signals as a function of abstract model signals, and thus provide a refinement map (i.e., a translation between abstraction levels). The low-level implementation of a signal must be simultaneously consistent with all of its abstract definitions. Thus, each abstract definition entails a verification task - to show that every implementation behavior is allowed by this definition. For the purpose of this verification task, one may use whichever abstract definition is most convenient for defining of the other signals. Suppose, for example, that we have abstract definitions of both the inputs and outputs of a given low-level block as a function of a high-level model, as depicted in figure 1. We can use the abstract definitions of the inputs to drive the inputs of the block from the high-level model when verifying that the outputs are consistent with their abstract definitions. Thus, the abstract model provides the context (or environment) for verifying the block, and we do not need to consider the remainder of the low-level model.
SMV also supports design by a successive refinement. One can define a sequence of layers, each of which is more detailed than the previous layer. The implementation of each signal is given by the lowest-level definition in the hierarchy.