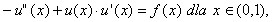
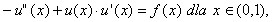
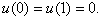
Dla prostoty, to równanie będziemy aproksymować metodą różnic skończonych, dostając problem dyskretny postaci:
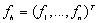znaleźć 
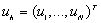spełniający
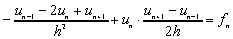dla 
,
.
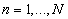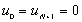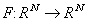. Oznaczając przez
uh wektor rozwiązania: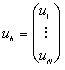
,możemy zapisać zagadnienie dyskretne w postaci wektorowej: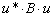 
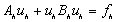,gdzie Ah oznacza macierz (minus) laplasjanu, a Bh macierz dyskretyzacji pierwszej pochodnej różnicą centralną, tzn.:
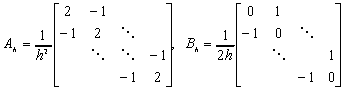
Zwróćmy uwagę, że tym razem operację mnożenia wektorów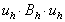 
rozumiemy nie w sensie iloczynu skalarnego, tylko jako operację mnożenia
odpowiadających współrzędnych.
Przy takim zapisie łatwo już określić funkcję, której zerem będzie rozwiązanie naszego zagadnienia:
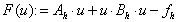
Jej pochodną będzie naturalnie taki operator liniowy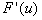 
,
który w działaniu na wektor w da wektor F'(u)w, określony
przez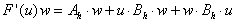 
. Określiliśmy
więc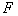 
oraz wyprowadziliśmy
wzór na F'. Jak pamiętamy, SNES będzie potrzebował procedur obliczających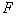 
i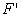
.
Musimy teraz zastanowić się, jak zaimplementować te funkcje w PETSc. Tutaj
pojawia się następna zaleta zapisu wektorowego: daje się on bardzo łatwo
"przetłumaczyć" na kod źródłowy PETSc!
Otóż przypuśćmy, że już zdefiniowaliśmy gdzieś w programie macierze Ah i Bh dyskretyzacji laplasjanu i pierwszej pochodnej (skądinąd doskonale wiemy, jak to zrobić!). Wtedy reszta to fraszka: wystarczy wygenerować wektor prawej strony i w procedurze zapisać, że wartość F(X) oblicza się w/g następującego algorytmu:
   |
 |
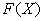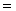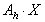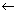macierz laplasjanu pomnożona przez X funkcją MatMult() |
 |
 |
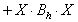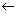wynik mnożenia macierzy pierwszej pochodnej przez X, razy (po współrzędnych) X - funkcje MatMult() oraz VecPointwiseMult(), |
 |
 |
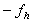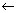prawa strona |
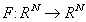możemy reprezentować jako macierz 
.
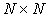Zwróćmy jednak uwagę na pewien detal: było nam wygodniej zapisać pochodną
F nie jako macierz pochodnych cząstkowych, lecz jako operator, którego
wartości na zadanym wektorze w są zdefiniowane pewnym wzorem. W
taki właśnie sposób definiuje się w PETSc macierze powłokowe (shell
matrices), o których była mowa na stronie 18. Idea macierzy powłokowych
wyjątkowo dobrze sprawdzi się w naszym zagadnieniu: /* uzyj A i B do obliczenia F */
MatMult(A); VecAXPY(); MatMult(B);
itd...
/* zwolnij macierze A i B */
MatDestroy(A); MatDestroy(B);
}
int main(int argc, char **argv)
{
/* generuj A i B, a nastepnie przypisz
im wartosci */
MatCreate(A); MatCreate(B);
MatSetValues(A); ...itd...
/* ......... */
SNESSetFunction( Funkcja );
/* ......... */
/* zwolnij macierze A i B */
MatDestroy(A); MatDestroy(B);
return(0);
}
/******************************************************
Procedura obliczajaca F(X)
******************************************************/
int Funkcja( SNES MojSnes, Vec X, Vec F, void
* Ctx )
{
/* uzyj A i B do obliczenia F */
MatMult(A); VecAXPY(); MatMult(B);
itd...
return(0);
}
To już jest całkiem dobre, a zwłaszcza - znacznie bardziej efektywne, niż poprzednia propozycja. Niemniej, kiedy wiemy, jak to zrobić efektywnie, powinniśmy spróbować zrobić to elegancko i temu właśnie będzie służył tytułowy koncept kontekstu użytkownika (pomysł na grę słów zaczerpnęliśmy od B.Smitha). Cóż, eleganckim rozwiązaniem byłoby przekazanie do Funkcji() macierzy Ah i Bh (uprzednio wygenerowanych na zewnątrz procedury mnożenia!) w postaci parametrów. Z tym jednak pozornie jest kłopot: format Funkcji() jest sztywny i nie możemy dowolnie modyfikować listy jej argumentów. Na szczęście, ostatnim dopuszczalnym argumentem funkcji jest wskaźnik do kontekstu użytkownika, zawierającego pomocnicze dla procedury obiekty i właśnie w ten sposób przekażemy nasze macierze!
Jak taki kontekst powinien wyglądać? Zasadniczo, będzie to struktura w C, zawierająca parametry, które zechcemy przekazać do Funkcji(). Tymi parametrami mogą być macierze, wektory robocze (o tak, przydadzą się!), a nawet wskaźniki do funkcji udostępniających zmienne lokalne funkcjom używającym naszego kontekstu. Taka struktura, ze zmiennymi lokalnymi, funkcjami dostępu itp. mocno pachnie porządną klasą w C++ i tak jest w rzeczywistości: programowanie z użyciem kontekstów ma wiele cech programowania obiektowego. Osoby dociekliwe z pewnością zauważyły, że typy (konteksty!) Vec, Mat,SLES itp. maja bardzo wiele cech regularnych klas w C++.
Wracając do naszej konkretnej sytuacji, kontekst, jaki chcielibyśmy przekazać do Funkcji(), powinien zawierać dwie macierze: dyskretyzacji laplasjanu i pierwszej pochodnej. Kontekst ma być strukturą, więc wygodnie nam będzie najpierw zdefiniować odpowiedni typ strukturalny:
typedef struct {
Mat A;
Mat B;
} USERCTX;
/* zwolnienie kontekstu */
USERCTXDestroy( &UserCtx );
}
}
static Scalar zero = 0.0;
static Scalar one = 1.0;
static Scalar mone = -1.0;
typedef struct
{
Mat Lap; /* macierz laplasjanu
*/
Mat Poch; /* macierz pierwszej pochodnej */
Vec X; /* wektor rozwiazania
*/
Vec F; /*
prawej strony */
Vec R; /*
residuum
*/
Vec y; /*
pomocniczy
*/
Vec z; /*
pomocniczy
*/
} USERCTX;
#include "snes.h" /* plik z definicjami funkcji
i obiektow SNES; zawiera takze
dyrektywe #include "sles.h" */
#include "user.h" /* kontekst uzytkownika i przydatne stale */
/******************************************************
Procedura obliczajaca wartosci funkcji F
******************************************************/
int Funkcja(SNES MojSnes,Vec X,Vec F,void
*Ctx)
{
int ierr;
USERCTX *UserCtx = (USERCTX *)Ctx;
/* Pomnoz przez pochodna centralna... */
ierr = MatMult( UserCtx->Poch, X, UserCtx->y ); CHKERRQ(ierr);
/* ...i domnoz przez u */
ierr = VecPointwiseMult( X, UserCtx->y,
F ); CHKERRQ(ierr);
/* Pomnoz przez laplasjan */
ierr = MatMult( UserCtx->Lap, X, UserCtx->y
); CHKERRQ(ierr);
/* Zsumuj! */
ierr = VecAXPY( &one, UserCtx->y,
F ); CHKERRQ(ierr);
ierr = VecAXPY( &mone, UserCtx->F,
F ); CHKERRQ(ierr);
return(ierr);
}
/******************************************************
Definicja pochodnej F
******************************************************/
#include "snes.h"
#include "user.h"
/* Implementacja funkcji Jakobian(), przekazywanej do SNESu */
int Jakobian(SNES MojSnes, Vec X, Mat *Jac,
Mat *Precond, MatStructure *flag, void *Ctx)
{
*flag = SAME_NONZERO_PATTERN;
return(0);
}
/* Implementacja mnozenia przez macierz jakobianu */
int MultJakobian( Mat Jac, Vec VecIn, Vec
VecOut )
{
int ierr;
USERCTX *UserCtx;
/* Najpierw musimy wydobyc kontekst
*/
ierr = MatShellGetContext( Jac, (void
**)&UserCtx );CHKERRQ(ierr);
/* Pomnoz przez pochodna centralna...
*/
ierr = MatMult( UserCtx->Poch, VecIn,
UserCtx->y ); CHKERRQ(ierr);
/* ...i domnoz przez u */
ierr = VecPointwiseMult( UserCtx->X,
UserCtx->y, VecOut ); CHKERRQ(ierr);
/* Pomnoz przez laplasjan */
ierr = MatMult( UserCtx->Lap, VecIn,
UserCtx->y ); CHKERRQ(ierr);
/* Zsumuj! */
ierr = VecAXPY( &one, UserCtx->y,
VecOut ); CHKERRQ(ierr);
ierr = MatMult( UserCtx->Poch, UserCtx->X,
UserCtx->y ); CHKERRQ(ierr);
ierr = VecPointwiseMult( VecIn, UserCtx->y,
UserCtx->z ); CHKERRQ(ierr);
ierr = VecAXPY( &one, UserCtx->z, VecOut ); CHKERRQ(ierr);
return(ierr);
}
#include <stdio.h>
#include <math.h> /* zawiera
funkcje sin(x) */
#include "snes.h"
#include "user.h"
static char help[] = "Rozwiazuje nieliniowe
jednowymiarowe rownanie\n\
konwekcji-dyfuzji na odcinku [0,L]\n\
Opcje: -N [int] liczba wewnetrznych wezlow
siatki\n\
-L [Scalar]
dlugosc odcinka\n\n";
/* Deklaracje procedur obliczajacych funkcje
i jakobian */
extern int MultJakobian( Mat, Vec, Vec);
int Jakobian(SNES,Vec,Mat*,Mat*,MatStructure*,void*);
int Funkcja(SNES,Vec,Vec,void*);
int USERCTXCreate(USERCTX*,int,Scalar);
int USERCTXDestroy(USERCTX*);
/**************************************************************
Program glowny
**************************************************************/
int main( int argc, char **argv )
{
SNES MojSnes;
/* obiekt SNES, ktorym rozwiazemy zadanie */
Mat
MatJ; /* macierz
jakobianu */
USERCTX UserCtx;
/* kontekst uzytkownika */
int
n;
/* liczba wezlow siatki */
static Scalar L = M_PI; /* dlugosc
przedzialu calkowania,
zatem krok siatki h = L/n */
int
ierr, flg, its;
PetscInitialize( &argc, &argv,PETSC_NULL,help
);
/* Interpretacja opcji uzytkownika
*/
ierr = OptionsGetInt( PETSC_NULL,
"-N", &n, &flg ); CHKERRA(ierr);
if( !flg ) n = 3;
ierr = OptionsGetScalar( PETSC_NULL,
"-L", &L, &flg );
CHKERRA(ierr);
/* Tworzenie potrzebnych obiektow:
SNESu, wektorow, macierzy pomocniczych */
ierr = SNESCreate(MPI_COMM_WORLD,SNES_NONLINEAR_EQUATIONS,&MojSnes);
CHKERRA(ierr);
ierr = USERCTXCreate( &UserCtx,
n, L ); CHKERRA(ierr);
VecView( UserCtx.F, VIEWER_DRAWX_WORLD
); PetscSleep(5);
/* Przekaz SNESowi funkcje i wektor
residualny */
ierr = SNESSetFunction(MojSnes, UserCtx.R,
Funkcja, &UserCtx); CHKERRA(ierr);
/* Przekaz SNESowi macierz jakobianu
i funkcje obliczajaca jakobian */
ierr = MatCreateShell(MPI_COMM_WORLD,n,n,n,n,&UserCtx,&MatJ);
CHKERRA(ierr);
ierr = MatShellSetOperation(MatJ,
MATOP_MULT, MultJakobian ); CHKERRA(ierr);
ierr = SNESSetJacobian(MojSnes,MatJ,MatJ,Jakobian,&UserCtx);
CHKERRA(ierr);
/* Uwzglednij opcje uruchomienia SNESu
typu -snes_view -snes_monitor */
ierr = SNESSetFromOptions(MojSnes);
CHKERRA(ierr);
/* Rozwiaz! */
ierr = SNESSolve(MojSnes,UserCtx.X,&its);
CHKERRA(ierr);
PetscPrintf(MPI_COMM_WORLD, "Liczba
iteracji = %d\n", its);
PetscPrintf(MPI_COMM_WORLD,"Wektor
rozwiazania:\n");
ierr = VecView(UserCtx.X, VIEWER_DRAWX_WORLD);
CHKERRA(ierr);
PetscSleep( 10 );
/* Zwolnij pamiec */
ierr = USERCTXDestroy(&UserCtx);
CHKERRA(ierr);
ierr = MatDestroy(MatJ); CHKERRA(ierr);
ierr = SNESDestroy(MojSnes); CHKERRA(ierr);
PetscFinalize();
return 0;
}
/**************************************************************
Funkcje zwiazane z kontekstem uzytkownika
**************************************************************/
int USERCTXCreate( USERCTX * UserCtx, int
n, Scalar L )
{
extern int GenerujLaplasjan1D( Mat, Scalar
);
extern int GenerujPochodnaCentralna1D( Mat,
Scalar );
int ierr=0;
int i;
double val;
double h = L/(n+1); /* krok siatki */
/* tworzymy wektory uzywane w kontekscie
naszego zagadnienia */
ierr = VecCreate(MPI_COMM_WORLD,PETSC_DECIDE,n,&UserCtx->X);
CHKERRQ(ierr);
ierr = VecDuplicate(UserCtx->X,&UserCtx->R);
CHKERRQ(ierr);
ierr = VecDuplicate(UserCtx->X,&UserCtx->F);
CHKERRQ(ierr);
ierr = VecDuplicate(UserCtx->X,&UserCtx->y);
CHKERRQ(ierr);
ierr = VecDuplicate(UserCtx->X,&UserCtx->z);
CHKERRQ(ierr);
/* tworzymy macierze uzywane w kontekscie
naszego zagadnienia */
ierr = MatCreate(MPI_COMM_WORLD,n,n,&UserCtx->Lap);
CHKERRQ(ierr);
ierr = MatCreate(MPI_COMM_WORLD,n,n,&UserCtx->Poch);
CHKERRQ(ierr);
/* generujemy elementy macierzy pomocniczych
*/
ierr = GenerujLaplasjan1D( UserCtx->Lap,
(Scalar) h ); CHKERRQ(ierr);
ierr = MatView( UserCtx->Lap, VIEWER_DRAWX_WORLD
); CHKERRQ(ierr);
PetscSleep( 3 );
ierr = GenerujPochodnaCentralna1D( UserCtx->Poch, (Scalar) h );CHKERRQ(ierr);
ierr = MatView( UserCtx->Poch, VIEWER_DRAWX_WORLD ); CHKERRQ(ierr);
PetscSleep( 3 );
/* generujemy prawa strone */
for( i = 1 ; i <= n ; i++ )
{
val = sin(i*h) + sin(i*h)*cos(i*h); /* rozwiazanie u(x) = sin(x) */
VecSetValue( UserCtx->F, i-1, (Scalar)val, INSERT_VALUES );
}
/* Przyblizenie poczatkowe */
/* Zakladamy, ze zerowe... Od razu
wpisujemy do wektora rozwiazania X */
ierr = VecSet(&zero, UserCtx->X);
CHKERRQ(ierr);
return(ierr);
}
int USERCTXDestroy( USERCTX * UserCtx )
{
int ierr;
ierr = VecDestroy(UserCtx->X); CHKERRQ(ierr);
ierr = VecDestroy(UserCtx->R); CHKERRQ(ierr);
ierr = VecDestroy(UserCtx->F); CHKERRQ(ierr);
ierr = VecDestroy(UserCtx->z); CHKERRQ(ierr);
ierr = VecDestroy(UserCtx->y); CHKERRQ(ierr);
ierr = MatDestroy(UserCtx->Lap); CHKERRQ(ierr);
ierr = MatDestroy(UserCtx->Poch);
CHKERRQ(ierr);
return(ierr);
}
PetscInitialize( &argc, &argv,PETSC_NULL,help ); /* Interpretacja opcji uzytkownika */ OptionsGetInt( PETSC_NULL, "-N", &n, &flg ); if( !flg ) n = 3; OptionsGetScalar( PETSC_NULL, "-L", &L, &flg );
/* Tworzenie potrzebnych obiektow: SNESu, wektorow, macierzy pomocniczych */ SNESCreate(MPI_COMM_WORLD,SNES_NONLINEAR_EQUATIONS,&MojSnes); USERCTXCreate( &UserCtx, n, L );
/* Przekaz SNESowi funkcje i wektor residualny */ SNESSetFunction(MojSnes, UserCtx.R, Funkcja, &UserCtx);
MatCreateShell(MPI_COMM_SELF,n,n,n,n,&UserCtx,&MatJ); MatShellSetOperation(MatJ, MATOP_MULT, MultJakobian );
SNESSetJacobian(MojSnes,MatJ,MatJ,Jakobian,&UserCtx);
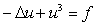, z jednorodnymi
warunkami brzegowymi Dirichleta.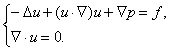
Wybór schematu numerycznego dla aproksymacji tego równania nie jest trywialny.
 |
 |
 |