Ergodic theory of meromorphic maps The theory of multifractal formalism, developed in the 1970s, provides a number of powerful tools for studying the geometry and ergodic properties of invariant hyperbolic repellers in the Julia set of rational functions on the Riemann sphere. The projects concerns extending the theory to the setup of transcendental entire and meromorphic maps. Within the previous work on the project, we have proved, among others, the Bowen formula for transcendental maps with a finite number of singular values (Ergodic Theory Dynam. Systems 32 (2012), no. 4, 1165-1189). This is a joint project with B. Karpińska (Warsaw University of Technology) and A. Zdunik (Uniwersity of Warsaw). In particular, the research was carried out within the Polish MNiSW / NCN grants N N201 0234 33 and N N201 607940.
	Topological properties of invariant sets in the dynamics of transcendental functions The project concerns the study of iteration of transcendental entire and meromorphic maps on the complex plane. We are interested in the relations between the dynamics of the map and the topology and geometry of invariant subsets, in particular the Julia set and the escaping set. Within the previous work on the project, we have proved an open conjecture concerning the connectivity of the Julia sets of Newton's method of finding zeroes of transcendental entire maps (Invent. Math. 198 (2014), no. 3, 591-636). This is a joint project with N. Fagella (Universitat de Barcelona), X. Jarque (Universitat de Barcelona) and B. Karpińska (Warsaw University of Technology), carried out within the Polish NCN grant HARMONIA 2012/06/M/ST1/00168.
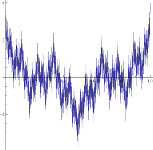
	Dimension of the graphs of the Weierstrass-type functions We study the ergodic properties of the graphs of non-differentiable real functions of the Weierstrass type. They are examples of invariant repellers of hyperbolic systems with two different positive Lyapunov exponents, i.e. two different speeds of expansion in unstable directions. They can also be regarded as limit sets (attractors) of some iterated function systems (IFS). Within the previous work on the project, we have proved a well-known open conjecture concerning the Hausdorff dimension of such graphs, stated by Mandelbrot in the 1980s (Adv. Math. 265 (2014), 32-59). This is a joint project with B. Bárány (Budapest University of Technology and Economics / Univerity of Warwick) and J. Romanowska (Uniwersity of Warsaw).