A Shared Memory Communication Protocol
Łukasz Bieniasz-Krzywiec
na podstawie "Distributed Systems Analysis with CCS" autorstwa G. Bruns'a
Plan
- Czym jest MSMIE?
- Złe pomysły
- Dobry pomysł
- Naturalny Model protokołu
- Sprawdzamy wymagania
- Abstrakcyjny Model protokołu
- Zapomniana własność
- Dobre Rozwiązanie
Plan
- Czym jest MSMIE?
- Złe pomysły
- Dobry pomysł
- Naturalny Model protokołu
- Sprawdzamy wymagania
- Abstrakcyjny Model protokołu
- Zapomniana własność
- Dobre Rozwiązanie
Czym jest MSMIE?
- Multiprocessor Shared-Memory Information Exchange
- protokół służący do komunikowania procesorów w systemach czasu rzeczywistego
- został zaprojektowany przez Westinghouse
- przeznaczenie: część systemu kontrolowania bezpieczeństwa elektrowni atomowych
- wdrożenie: Sizewell B Reactor w Wielkiej Brytani
Składowe systemu
- Master Processor (wykonujący obliczenia)
- Slave Processor (wykonujący pomiary)
- System Bus
- Shared Memory
Schemat Systemu
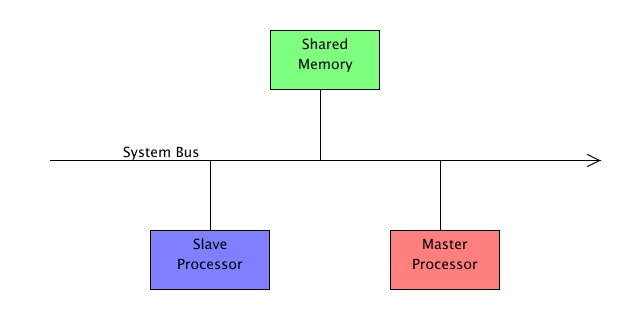
Wymagania
- nic nie możemy założyć o tempie działania procesorów
- niedozwolone jest czytanie z bufora, do którego własnie ktoś pisze (data tearing)
- narzut związany z komunikacją musi być określony i możliwie mały
Uproszczenia
- komunikacja jednostronna
Slave Processor -> Master Processor - z każdym buforem związany jest dokładnie jeden Slave Processor i dwa Master Processors
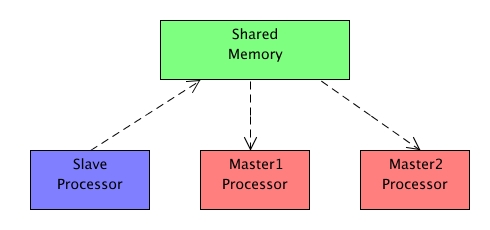
Plan
- Czym jest MSMIE?
- Złe pomysły
- Dobry pomysł
- Naturalny Model protokołu
- Sprawdzamy wymagania
- Abstrakcyjny Model protokołu
- Zapomniana własność
- Dobre Rozwiązanie
Zły pomysł [1/2]
- jeden bufor w pamięci dzielonej
- wyłączność dostępu gwarantowana semaforem
Wady to opóźnienia:
- gdy Master czeka aż Slave skończy pisać
- gdy Slave czeka aż Master skończy czytać
Zły pomysł [2/2]
- dwa bufory w pamięci dzielonej
- możliwe statusy buforów: slave, newest, master, idle
- wyłączność dostępu do statusu gwarantowana semaforem
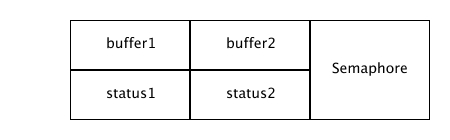
Wady to znów opóźnienia.
Plan
- Czym jest MSMIE?
- Złe pomysły
- Dobry pomysł
- Naturalny Model protokołu
- Sprawdzamy wymagania
- Abstrakcyjny Model protokołu
- Zapomniana własność
- Dobre Rozwiązanie
Dobry pomysł
- dokładamy trzeci bufor
- statusy buforów: slave, newest, master, idle
- pamiętamy liczbę aktualnie czytających procesorów: counter
- wyłączność dostępu do statusu i licznika gwarantowana semaforem
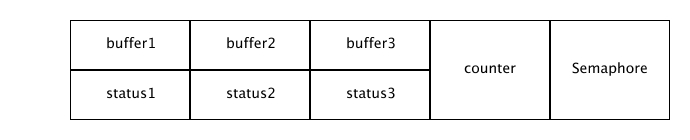
Slave write
- Zdobądź semafor.
- Jeśli jest bufor newest, to zmień jego status na idle.
- Jeśli jest bufor slave, to zmień jego status na newest.
Wpp. BŁĄD - Jeśli jest bufor idle, to zmień jego status na slave.
Wpp. BŁĄD - Oddaj semafor.
Master Acquire
- Zdobądź semafor.
- Jeśli jest bufor newest i nie ma bufora master,
to zmień status bufora newest na master. - Jeśli jest bufor master, to zwiększ liczbę czytających procesorów.
- Oddaj semafor.
Master Release
- Zdobądź semafor.
- Zmniejsz liczbę czytających procesorów.
- Jeśli liczbę czytających procesorów == 0, to
- Jeśli jest bufor newest, to zmień status bufora master na idle.
- Wpp. zmień status bufora master na newest.
- Oddaj semafor.
Kilka własności
- w pamięci jest zawsze dokładnie 1 bufor slave
- w pamięci jest zawsze co najwyżej 1 bufor newest
- w pamięci jest zawsze co najwyżej 1 bufor master
- data tearing niemożliwy dzięki semaforowi
- Slave może pisać kiedy zechce
- Master może czytać o ile Slave wyknał co najmniej 1 zapis
Plan
- Czym jest MSMIE?
- Złe pomysły
- Dobry pomysł
- Naturalny Model protokołu
- Sprawdzamy wymagania
- Abstrakcyjny Model protokołu
- Zapomniana własność
- Dobre Rozwiązanie
Interfejs
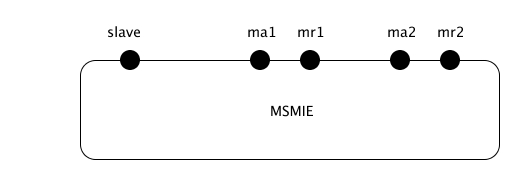
- czy system się blokuje?
- czy konkretne akcje są zawsze możliwe do wykonania?
- czy dane zapisane przez Slave są poprawnie odczytane przez Master?
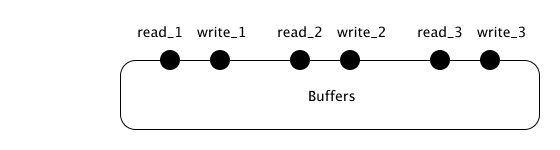
Bufory
Buf(s) = 'read(s).Buf(s) + write(s').Buf(s') Buf_i(s) = Buf(s)[read_i/read, write_i/write] Buffers = Buf_1(s) | Buf_2(i) | Buf_3(i)
Counter i Semaphore
Counter(n) = (if n = 0 then zero.Counter(n))
+ (if n < 2 then inc.Counter(n + 1))
+ (if n > 0 then dec.Counter(n - 1))
Semaphore = take.give.Semaphore
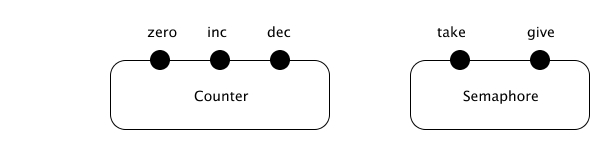
MemImage = Buffers | Counter(0) | Semaphore
Slave
Slave = slave.Sl1
Sl1 = 'take.read_1(v1).read_2(v2).read_3(v3).Sl2((v1,v2,v3))
Sl2(B) = sum(i:{1,2,3}, if B#i = N then Sl3(B[i -> I]))
+ if N not in {B#1, B#2, B#3} then Sl3(B)
Sl3(B) = sum(i:{1,2,3}, if B#i = S then Sl4(B[i -> N]))
Sl4(B) = sum(i:{1,2,3}, if B#i = I then Sl5(B[i -> S]))
Sl5(B) = 'write_1(B#1).'write_2(B#2).'write_3(B#3).'give.Slave
Master Acquire
Master = MA1
MA1 = 'take.read_1(v1).read_2(v2).read_3(v3).MA2((v1,v2,v3))
MA2(B) = if N in {B#1, B#2, B#3} and M not in {B#1, B#2, B#3}
then sum(i:{1,2,3}, if B#i = N then MA3(B[i -> M]))
else MA3(B)
MA3(B) = (if M in {B#1, B#2, B#3} then ma.'inc.MA4(B))
+ 'give.Master
MA4(B) = 'write_1(B#1).'write_2(B#2).'write_3(B#3).'give.MR1
Master Release
MR1 = mr.'take.read_1(v1).read_2(v2).read_3(v3).MR2((v1,v2,v3))
MR2(B) = 'dec.MR3(B)
MR3(B) = 'zero.(sum(i:Bid, if B#i = M
then (if N in {B#1, B#2, B#3}
then MR4(B[i -> I])
else MR4(B[i -> N]))))
+ 'dec.'inc.MR4(B)
MR4(B) = 'write_1(B#1).'write_2(B#2).'write_3(B#3).'give.Master
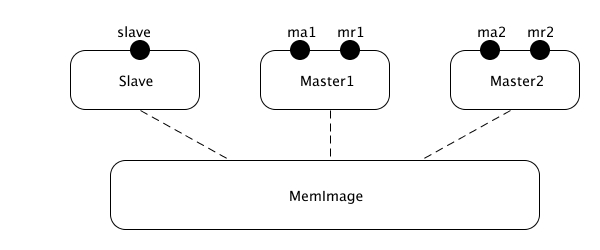
Z lotu ptaka
Master_k = Master[ma_k/ma, mr_k/mr] Msmie = (MemImage | Slave | Master_1 | Master_2) \ L
Plan
- Czym jest MSMIE?
- Złe pomysły
- Dobry pomysł
- Naturalny Model protokołu
- Sprawdzamy wymagania
- Abstrakcyjny Model protokołu
- Zapomniana własność
- Dobre Rozwiązanie
Sprawdzamy wymagania [1/2]
- data tearing - OK
-
Czy Slave zawsze może pisać do bufora?Czy akcję slave można zawsze wykonać?
Always(A) = max(X.A & [[-]]X)
SlaveAlwaysPossible = Always(<<slave>>T)
OK
Sprawdzamy wymagania [2/2]
-
Czy Master zawsze może czytać z bufora?Czy akcje ma, mr można zawsze wykonać?
MasterAlwaysPossible =
[[slave]]Always(<<ma1,mr1>>T & <<ma2,mr2>>T)
OK
Plan
- Czym jest MSMIE?
- Złe pomysły
- Dobry pomysł
- Naturalny Model protokołu
- Sprawdzamy wymagania
- Abstrakcyjny Model protokołu
- Zapomniana własność
- Dobre Rozwiązanie
Slave actions
- M({(s,l1), (n,l2), (i,l3)}, r) - slave → M({(n,l1), (s,l2), (i,l3)}, r)
- M({(s,l1), (n,l2), (i,l3)}, r) - slave → M({(n,l1), (i,l2), (s,l3)}, r)
- M({(s,l1), (i,l2)} + B', r) - slave → M({(n,l1), (s,l2)} + B', r)
gdzie, (n,_) not in B' - M({(s,l1), (n,l2)} + B', r) - slave → M({(n,l1), (s,l2)} + B', r)
gdzie, (i,_) not in B'
Master acquire actions
Dla k = 1,2- M({(m,l)} + B', r) - ma_k → M({(m,l)} + B', r + {k})
gdzie, k not in r - M({(n,l)} + B', Ø) - ma_k → M({(m,l)} + B', {k})
gdzie, (m,_) not in B'
Master release actions
Dla k = 1,2- M({(m,l)} + B', r + {k}) - mr_k → M({(m,l)} + B', r)
gdzie, r != Ø, k not in r - M({(m,l1), (n,l2)} + B', {k}) - mr_k → M({(i,l1), (n,l2)} + B', Ø)
- M({(m,l)} + B', {k}) - mr_k → M({(n,l)} + B', Ø)
gdzie, (n,_) not in B'
Wersja Minimalna MSMIE
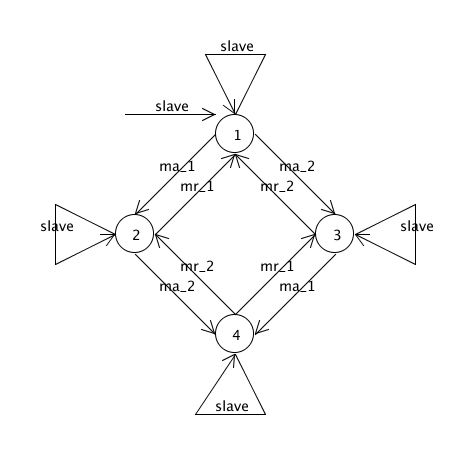
Ups...

Plan
- Czym jest MSMIE?
- Złe pomysły
- Dobry pomysł
- Naturalny Model protokołu
- Sprawdzamy wymagania
- Abstrakcyjny Model protokołu
- Zapomniana własność
- Dobre Rozwiązanie
Drobna zmiana
Dla k = 1,2- M({(n,l)} + B', Ø) - ma'_k → M({(m,l)} + B', {k})
gdzie, (m,_) not in B'
ma'_k oznacza zaczęcie czytania z bufora o statusie newest.
Zmieniona Wersja Minimalna MSMIE
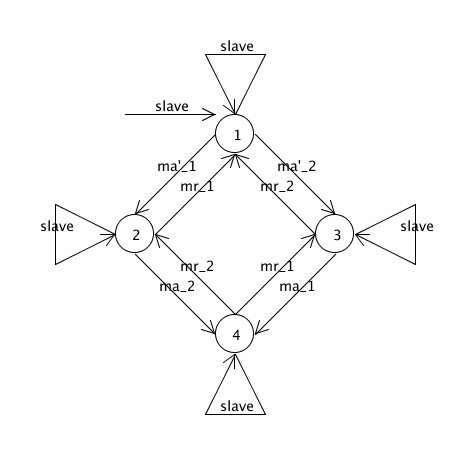
Zapomniana własność
Dane zapisane przez Slave zostaną w końcu odczytane.
Nasz model nie ma tej własności, bo nie mamy żadnej pewności, że akcje Master występują.
Jeśli Master actions będą ciągle występować, to dane zapisane przez Slave zostaną w końcu odczytane.
Jak opisać tę własność formułą?
Kluczowa Formuła [1/2]
Rozważmy proces z sort równym {a, b, c}.-
Jak wyrazić formułą, że akcja a musi kiedyś zajść?
min(X. <->T & [b,c]X)
min(X. <<-eps>> & [[b,c]]X) -
Jak wyrazić formułą, że akcja a musi kiedyś zajść, jeśli akcje b ciągle występują?
min(X.max(Y.<<-eps>>T & [[c]]Y & [[b]]X));
Kluczowa Formuła [2/2]
-
Jak wyrazić formułą, że akcja a musi kiedyś zajść, jeśli akcje b1 oraz b2 ciągle występują?
min(X.max(Y1.<<-eps>>T & [[c,b2]]Y1 & [[b1]] max(Y2.<<-eps>>T & [[c,b1]]Y2 & [[b2]]X)));
Fair = min(X.max(Y1.<<-eps>>T & [[mr1,mr2,slave,ma2]]Y1 & [[ma1]]
max(Y2.<<-eps>>T & [[mr1,mr2,slave,ma1]]Y2 & [[ma2]]X)));
ValuesPassed = Always([[slave]]Fair);
Plan
- Czym jest MSMIE?
- Złe pomysły
- Dobry pomysł
- Naturalny Model protokołu
- Sprawdzamy wymagania
- Abstrakcyjny Model protokołu
- Zapomniana własność
- Dobre Rozwiązanie
Nowe MSMIE
- cztery bufory w pamięci dzielonej
-
możliwe statusy buforów:
slave, newest, master, old, idle - Master nigdy nie zaczyna czytać z bufora old
- bufor old przestanie być zatem kiedyś używany
Nowe Master Acquire
- Jeśli nie ma bufora master, to zmień status bufora newest na master i zacznij z niego czytać.
-
Jeśli bufor b1 ma status master i bufor b2 ma status newest i nie ma bufora old, to:
- zmień status bufora b1 na old,
- zmień status bufora b2 na master i zacznij z niego czytać.
- Jeśli bufor b ma status master oraz nie ma bufora newest lub jest bufor old, to zacznij czytać z bufora b.