No Title

Matematyka B, wykład 8. z dn. 6.11.2000

Potrzebne nam będą dodatkowe pojęcia.

Def 1. Niech V_i, $i\in I$ będą podprzestrzeniami p.w. Vsumę algebraiczną $\sum_{i\in I} V_i$ nazywa się sumą prostą jeśli każdy element v tej sumy algebraicznej można przedstawić jednoznacznie w postaci

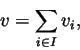
$\begin{displaymath}v=\sum_{i\in I} v_i, \end{displaymath}$

gdzie $v_i\in V_i$ . Piszemy $\bigoplus_{i\in I} V_i$ .

Stw 1. Załóżmy, że V_i są podprzestrzeniami p.w. V. Wtedy

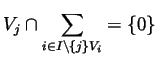
$\displaystyle{\sum_{i\in I} V_i}$ jest sumą prostą w.t.w. dla każdego $j\in I$ , $\displaystyle{V_j\cap \sum_{i\in I\setminus\{j\} V_i}=\{0\}}$

D.: $\Rightarrow$ a.a. Niech istnieje j t.że

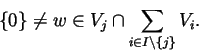
$\begin{displaymath}\{0\} \neq w\in V_j\cap \sum_{i\in I\setminus\{j\} }V_i. \end{displaymath}$

Zatem $w =\sum_{i\in I\setminus\{j\}} w_i$ , gdzie $w_i\in V_i$ . Wtedy kładziemy:

$\begin{displaymath}v_i=\cases{w_i, & gdy $i\neq j$\cr 0, & gdy $i=j$}\qquad v'_i=\cases{0& gdy $i\neq j$\cr w, & gdy $i=j$.} \end{displaymath}$

w ma dwa różne przedstawienia:

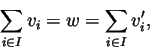
$\begin{displaymath}\sum_{i\in I} v_i = w =\sum_{i\in I} v'_i , \end{displaymath}$

co daje sprzeczność.

$\Leftarrow$ , a.a. Jeśli $\sum_{i\in I} V_i$ nie jest sumą prostą, to istnieją $\{v_i\}$ i $\{v'_i\}$ , t.że v_i i v'_inależą do V_i i dla pewnego k, $v_k\neq v'_k$ . Zatem

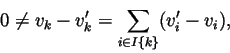
$\begin{displaymath}0\neq v_k-v'_k = \sum_{i\in I\{k\}}(v'_i-v_i), \end{displaymath}$

to znaczy, że istnieje niezerowy element przecięcia V_k i $\sum_{i\in I\{k\}}V_i$ . Otrzymana sprzeczność kończy dowód.

Def 2. Niech V₁, V₂ będą podprzestrzeniami p.w. Vi $V=V_1\oplus V_2$ , to wtedy powiemy, że V₂ (odpow. V₁) jest dopełnieniem V₁ (odpow. V₂). Kowymiarem (współwymiarem) V₁ nazywamy wymiar podprzestrzeni do niej dopełniajacej, piszemy $\hbox{codim}\, V_1$ .

Przykład. Niech V₁ będzie prostą w ${\bf R}^3$ przechodzącą przez początek układu współrzędnych a V₂niech będzie płaszczyzną, która nie zawiera V₁. Wtedy $V_1\oplus V_2$ i $\hbox{codim}\, V_1 =2$ i $\hbox{codim}\, V_2=1$ .

Def 3. Niech V będzie p.w. a W jej podprzestrzenią wektorową. Wprowadzamy relację równoważności wzorem $v \rho w$ w.t.w. $v-w\in W$ . Zamiast pisać $V/\rho$ będziemy używać oznaczenia: V/W.

Przykład. Przy oznaczeniach powyższego przykładu niech $V={\bf R}^3$ , W=V₁, wtedy łatwo się przekonać, że V/Wmożna utożsamiać z V₂. Uwaga: to nie jest ten sam obiekt.

Def 4. Niech V_i $i=1,\ldots, n$ będą p.w. W zbiorze $W:= V_1\times V_2\times\ldots\times V_n$ można wprowadzić działania. Jeśli $v, w\in W$ , to kładziemy

$\begin{displaymath}v+w = u,\quad \lambda v = t, \end{displaymath}$

gdzie

$\begin{displaymath}v=(v_1,\ldots, v_{n}),\quad w=(w_1,\ldots, w_{n}) \quad u=(u_1,\ldots, u_{n}) \quad t=(t_1,\ldots, t_{n}) \end{displaymath}$

$\begin{displaymath}u_i =v_i+w_i,\quad t_i =\lambda v_i. \end{displaymath}$

Stw 2. Z tak określonymi działaniami W jest p.w. nad ${\bf K}$ .

Możemy teraz omówić ważny przykład przestrzeni wektorowej:

§Przestrzeń wektorowa macierzy.

Def 5. Macierzą nad ciałem ${\bf K}$ o wymiarach $m\times n$ nazywamy dowolną funkcję $A:\{1,\ldots, m\}\times\{1,\ldots, n\} \to {\bf K}$ . Piszemy $A=\{a_{ij}\}$ , $i=1,\ldots, m,$ $j=1,\ldots, n$ . Zbiór macierzy $m\times n$ oznaczamy przez $M_{m\times n}({\bf K})$ .

Zauważmy jeszcze, że w $M_{m\times n}({\bf K})$ można w naturalny sposób wprowadzić działania dodawania i mnożenia przez liczbę: Jeśli A, B są macierzami, to

$\begin{displaymath}A+B =: C,\quad \lambda A=: D, \end{displaymath}$

gdzie

$\begin{displaymath}C=\{c_{ij}\}, \quad c_{ij}= a_{ij}+b_{ij},\qquad D=\{d_{ij}\}, \quad d_{ij} =\lambda a_{ij}. \end{displaymath}$

Łatwo się przekonać, że $M_{m\times n}({\bf K})$ z tak określonymi działaniami jest p.w. nad ${\bf K}$ .

Macierz kwadratową $\{a_{ij}\}$ , $i,j=1,\ldots,n$ nazywa się jednostkową, jeśli

$\begin{displaymath}a_{ij}=\cases{1,& gdy $i=j$\cr 0,& w przeciwnym przypadku.} \end{displaymath}$

Piszemy I (lub Id) i mówimy też, że I jest macierzą tożsamościową lub identycznościową. Później się przekonamy, że nazwa ``macierzy tożsamościowej'' jest w pełni uzasadniona.

Niech będzie dana macierz $A\in M_{m\times n}({\bf K})$ , wtedy macierze $C_j\in M_{m\times 1}({\bf K})$ , $j=1,\ldots, n$ i $R_i\in M_{1\times n}({\bf K})$ , $i=1,\ldots,m$ ,

$\begin{displaymath}C_j=\left[\matrix{ a_{1j}\cr \vdots \cr a_{1m}}\right], \quad R_i=\left[ a_{i1} \ldots a_{in}\right] \end{displaymath}$

nazywamy odpowiednio j-tą kolumną i i-tym wierszem.

Będziemy jeszcze potrzebowali definicji $T:M_{m\times n}({\bf K})\to M_{n\times m}({\bf K})$ , piszemy A^T. Jeśli $A=\{a_{ij}\},$ to A^T=B, gdzie $B= \{b_{ij}\}$ i b_ij=a_ji. Macierz A^T nazywamy macierzą transponowaną macierzy A. Zauważmy, że (A^T)^T=A.

Wprowadzimy teraz kolejne ważne pojęcie:

Def 6. Rzędem kolumnowym (wierszowym) macierzy A nazywa się ilość jej lnz kolumn (wierszy).

Będziemy badać (liczyć) rzędy macierzy, do tego celu przydatne jest poniższe stwierdzenie.

Stw 3. Niech $C_1,\ldots, C_n$ (odpowiednio: $R_1,\ldots,R_m$ ) będą kolumnami (odpowiednio: wierszami) macierzy A. Wtedy rząd kolumnowy (odpow: wierszowy) macierzy jest równy kowymiarowi w Kⁿ (odpow: w K^m) podprzestrzeń złożonej z rozwiązań

$\begin{displaymath}\left[\matrix{x_1\cr\vdots\cr x_n}\right]\quad \left(\left[\matrix{x_1\cr\vdots\cr x_m}\right]\right) \end{displaymath}$

r-nia

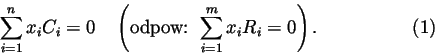
$\begin{displaymath}\sum_{i=1}^nx_i C_i =0 \quad\left(\hbox{odpow: } \sum_{i=1}^mx_iR_i =0\right).\eqno(1) \end{displaymath}$

Dowód przeprowadzimy dla wersji kolumnowej. Wiemy, że rozwiązania (1) tworzą podprzestrzeń wektorową. Niech rząd kolumnowy Awynosi k i kolumny $\{C_{n-k+1},\ldots,C_n\}$ są lnz. Możemy (1) przepisać w postaci

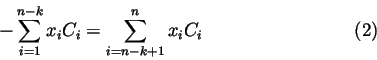
$\begin{displaymath}-\sum_{i=1}^{n-k} x_iC_i = \sum_{i=n-k+1}^n x_iC_i \eqno(2) \end{displaymath}$

Dla ustalonego $j\in\{1,\ldots,n-k\}$ kładziemy x_j=1 i x_i=0 dla $i\neq$ i $1\le i\le n-k$ , tj. (2) przyjmuje postać

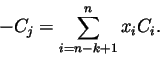
$\begin{displaymath}-C_j =\sum_{i=n-k+1}^n x_iC_i . \end{displaymath}$

Na mocy liniowej niezależności C_j, $n-k+1\le j \le n$ liczby x_i w r-niu wyżej są wyznaczone jednoznacznie i oznaczymy je $x_{n-k+1}^j,\ldots,x_n^j$ , tj. dla każdego j mamy rozwiązanie v_j r-nia (2):

$\begin{displaymath}v_j=(0, \ldots,0,1,0,\ldots,0, x_{n-k+1}^j,\ldots,x_n^j)^T, \end{displaymath}$

gdzie jedynka jest na j-tym miejscu. Oczywiście zbiór wektorów v_j, $1\le j\le n-k$ jest lnz. Jeśli $v=(\al_1,\ldots, \al_{n})$ jest rozwiązaniem, to

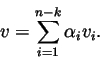
$\begin{displaymath}v= \sum_{i=1}^{n-k} \alpha_i v_i. \end{displaymath}$

Zauważmy, że wektor

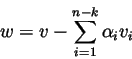
$\begin{displaymath}w=v- \sum_{i=1}^{n-k} \alpha_i v_i \end{displaymath}$

spełnia (2) i ma postać

$\begin{displaymath}(0,\ldots,0,\beta_{n-k+1},\ldots,\beta_n), \end{displaymath}$

skoro spełnia (2) to z liniowej niezależności C_jdostajemy, że $\beta_k=0$ , $n-k+1\le k\le n$ , tj. $\{v_i\}_{i=1}^{n-k}$ jest bazą podprzestrzenie rozwiązań (2), jej kowymiar jest równy k. c.k.d.

Wynika stąd prosty wniosek:

Stw 4. Rząd wierszowy macierzy A jest równy jej rzędowi kolumnowemu.

D.: Niech $A=\{a_{ij}\}$ i $R_1,\ldots,R_n$ będą wierszami zaś $C_1,\ldots,C_m$ kolumnami i rząd wierszowy to r i rząd kolumnowy to c. Niech $\{R_{i_1},\ldots,R_{i_r}\}$ będą wierszami lnz. Wtedy rzędy macierzowe macierzy

$\begin{displaymath}A=\left[\matrix{R_1\cr\vdots\cr R_m}\right],\quad B=\left[\matrix{R_{i_1}\cr\vdots\cr R_{i_r}}\right] \end{displaymath}$

są równe. W myśl poprzedniego stierdzenia rząd kolumnowy A wyznaczony jest przez rozwiązania układu

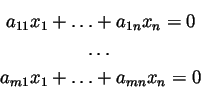
$\begin{eqnarray*}&a_{11}x_1+\ldots+a_{1n}x_n =0\\ &\dots\\ &a_{m1}x_1+\ldots+a_{mn}x_n =0\\ \end{eqnarray*}$

a rząd kolumnowy B wyznaczony jest przez rozwiązania układu

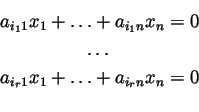
$\begin{eqnarray*}&a_{i_11}x_1+\ldots+a_{i_1n}x_n =0\\ &\dots\\ &a_{i_r1}x_1+\ldots+a_{i_rn}x_n =0\\ \end{eqnarray*}$

Jes oczywiste, że drugi układ postaje z wykreślenia równań, które są liniowo zależne. Łatwo się przekonać, że oba zbioru rozwiązań są równe. Wiedząc, że rzędy kolunowe A i B są równe, zauważmy, że rząd kolumnowy B wynosi najwyżej r. Wynika to stąd, że kolumy B są elementami ${\bf K}^r$ i dim ${\bf K}^r=r$ . Zatem $c\le r$ ten sam argument zastosowany do A^T daje $r\le c$ i ostatecznie r=c, co należało wykazać.

Dzięki temu stwierdzeniu poniższe określenie jest poprawne:

Def 7. Rzędem macierzy nazywamy jej rząd kolumnowy lub rzędowy.

Na koniec zanotujmy:

Stw 5. Rząd macierzy nie zmieni się, jeśli:

(a) do wiersza (kolumny) dodamy inny wiersz (kolumnę);

(b) wiersz (kolumnę) pomnożymy przez liczbę różną od zera;

About this document ...

Next: About this document ...

Piotr Rybka
2000-11-10