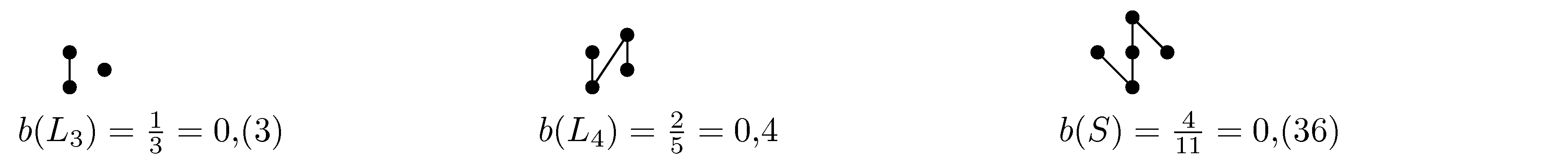
Conjecture (GPC) For every finite poset P, not a chain, we can point out two consecutive comparisons such that regardless of their results the inequality t0 ≥ t1 + t2 holds, where t0 denotes the number of linear extensions of the poset P and t1, t2 denotes the number of linear extensions of the poset obtained after the first comparison and after both comparisons, respectively.
The GPC implies the 1/3–2/3 Conjecture.
Let S(P) be the minimum number of comparisons that will suffice to sort the poset P. Let e(P) be the number of linear extensions of the poset P. The name of the GPC comes from the inequality S(P) ≤ logφe(P) it implies. Informally this means that during sorting process the number of linear extensions can be decreased in every comparison on average by at least golden ratio φ = (1 + √5)⁄2 ≈ 1.618.
We proved the GPC for posets of width two, semiorders and posets containing sufficiently many of minimal or maximal elements [P06b]. We also proved that the fraction of partial orders on an n-element set satisfying the GPC converges to 1 when n approaches infinity [P06b]. Using computers, we verified the GPC for all posets containing at most 11 elements [P06b] and we proved it for 6-thin posets [P08]. The proof took 787 hours of CPU time [ICM]. For details see also [PHD].
For a poset P = (X, <), let the balance constant b(P) be the maximum, over all pairs x, y ∈ X of min{Pr(x < y), Pr(y < x)}, where Pr(x < y) is the fraction of linear extensions in which x precedes y. We ask about n-element poset which is not a linear sum of another posets and has the smallest balance constant. We call such poset the worst balanced poset. The worst balanced posets for n = 3, 4, 5 are easy to find. They are illustrated in the following figure.
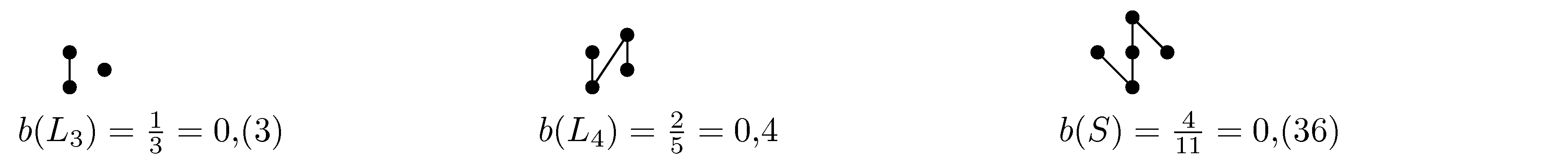
For n = 7, the worst balanced poset M7 first appears in this context in Saks [Order 2 (1985) 327–330]. All worst balanced posets for n = 6, 7, 8 are presented by Brightwell [Discr. Math. 201 (1999) 25–52] (however for n = 6 the figure there seems to be false). They are illustrated below.
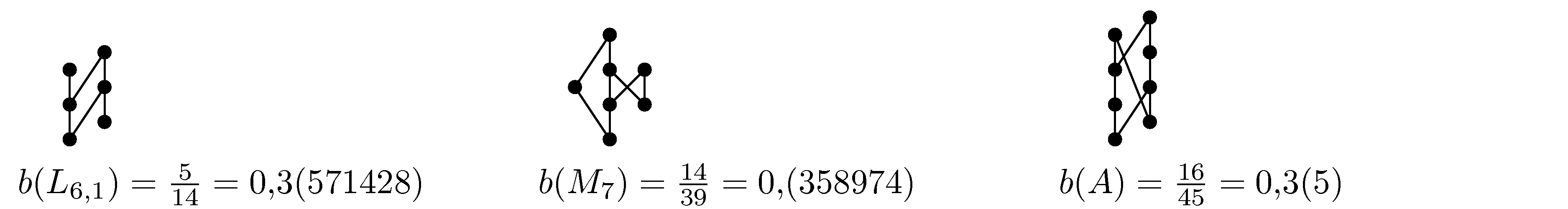
Using computer, we found the worst balanced posets for n = 9, 10, 11 [PHD]. They are illustrated in the following figure.
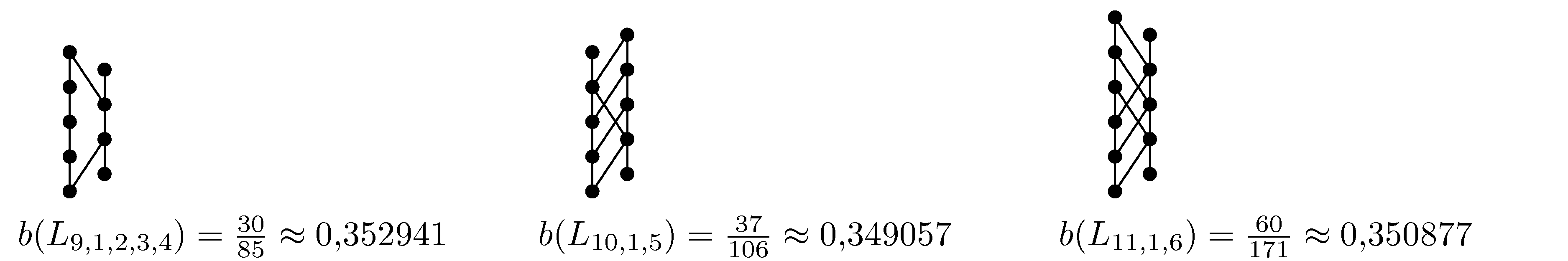
Observed regularity in the above figures leads us to define a new class of badly balanced posets, which we call ladders with broken rungs. The worst balanced posets with balance constant bigger than 1⁄3, we currently know, are in fact ladders with broken rungs and are illustrated in the following figure.
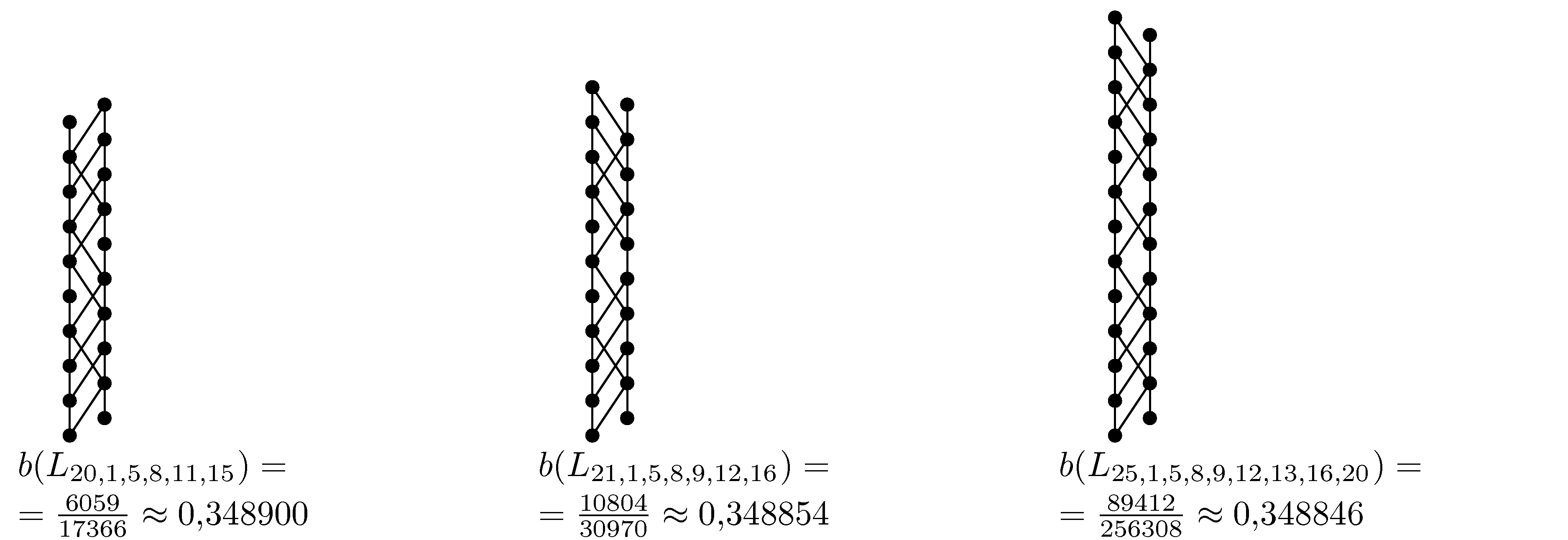
Let S(n) be the minimum number of comparisons that will suffice to sort n elements. Donald Knuth posed the problem of finding the value of S(13) in his classic book [The Art of Computer Programming, exercise 5.3.1.35, Sztuka programowania, zadanie 5.3.1.35].
2002: It turns out that S(13) = 34 [P02, MSC2]. The experiment took 10.5 hours on the personal computer equipped with 233 MHz processor and 64 MB memory.
10/12/2002: The recently finished experiment shows that S(22) = 71 [P04].
30/01/2003: The latest result is that S(14) = 38 [P04, PHD]. The improved method needs only 41 minutes on 650 MHz processor to complete the experiment for 13 elements.
12/12/2004: It turns out that S(15) = 42 [P07, PHD]. The computation took 17,554 hours of CPU time [ICM].
16/11/2005: For n < 47 there is no algorithm of the following form: ``m and n − m elements are sorted using the Ford–Johnson algorithm first, then the sorted sequences are merged'', whose total number of used comparisons is smaller than the number of comparisons used by the Ford–Johnson algorithm to sort n elements directly [P07, PHD, ICM].
The program gpc_phd proves the GPC for k-thin posets. The program was used in [PHD].
The program gpc also proves the GPC for k-thin posets. The actual version of the program used in [P08].
The program proof does experiments for posets with the particular number of elements.
Generalized black-peg Mastermind
Constant size memory Mastermind
Computing pancake blocks in [P26]
| [MSC1] | M. Peczarski, Metody, algorytmy i programy estymacji częstotliwości sygnałów sinusoidalnych w obecności zakłóceń (Methods, algorithms and programs for estimation of the sinusoidal signals frequency in presence of noise), MSc thesis, Warsaw University of Technology, Warsaw 1992 |
| [MSC2] | M. Peczarski, Optymalne sortowanie – eksperymenty (Optimal sorting—experiments), MSc thesis, University of Warsaw, Warsaw 2002 |
| [PHD] | M. Peczarski, Komputerowo wspomagane badanie zbiorów częściowo uporządkowanych (Computer assisted research of posets), PhD thesis, University of Warsaw, Warsaw 2006, Abstract |
| [Habilitation] | M. Peczarski, Komputerowo wspomagana analiza złożoności problemów algorytmicznych na przykładach gry Mastermind i sortowania przez porównywanie (Computer assisted complexity analysis of algorithmic problems on the examples of the Mastermind game and comparison sorting), 2021 |
| [P02] | M. Peczarski, Sorting 13 elements requires 34 comparisons, Algorithms – ESA 2002, 10th Annual European Symposium, Rome, Italy, September 17–21, 2002, Proceedings, R. Möring and R. Raman (Eds.), Lecture Notes in Computer Science 2461, 785–794, 2002, https://doi.org/10.1007/3-540-45749-6 |
| [P04] | M. Peczarski, New results in minimum-comparison sorting, Algorithmica 40 (2), 133–145, 2004, https://doi.org/10.1007/s00453-004-1100-7 |
| [P04e] | M. Peczarski, Strategy in Ulam's game and tree code give error-resistant protocols, 2004, https://arxiv.org/abs/cs/0410043 |
| [P06a] | M. Peczarski, An improvement of the tree code construction, Information Processing Letters 99 (3), 92–95, 2006, https://doi.org/10.1016/j.ipl.2006.03.007 |
| [P06b] | M. Peczarski, The Gold Partition Conjecture, Order 23 (1), 89–95, 2006, https://doi.org/10.1007/s11083-006-9033-1 |
| [P07] | M. Peczarski, The Ford–Johnson algorithm still unbeaten for less than 47 elements, Information Processing Letters 101 (3), 126–128, 2007, https://doi.org/10.1016/j.ipl.2006.09.001 |
| [P08] | M. Peczarski, The Gold Partition Conjecture for 6-thin posets, Order 25 (2), 91–103, 2008, https://doi.org/10.1007/s11083-008-9081-9 |
| [JP09] | G. Jäger, M. Peczarski, The number of pessimistic guesses in Generalized Mastermind, Information Processing Letters 109 (12), 635–641, 2009, https://doi.org/10.1016/j.ipl.2009.02.016 |
| [JP11] | G. Jäger, M. Peczarski, The number of pessimistic guesses in Generalized Black-peg Mastermind, Information Processing Letters 111 (19), 933–940, 2011, https://doi.org/10.1016/j.ipl.2011.06.009 |
| [P12] | M. Peczarski, Towards optimal sorting of 16 elements, Acta Universitatis Sapientiae, Informatica 4 (2), 215–224, 2012, https://acta.sapientia.ro/en/series/informatica/publications/informatica-contents-of-volume-4-number-2-2012/towards-optimal-sorting-of-16-elements, 2011, https://arxiv.org/abs/1108.0866 |
| [JP14] | G. Jäger, M. Peczarski, Playing several variants of Mastermind with constant-size memory is not harder than with unbounded memory, Combinatorial Algorithms, 25th International Workshop, IWOCA 2014, Duluth, MN, USA, October 15–17, 2014, Revised Selected Papers, J. Kratochwíl, Mirka Miller, Dalibor Froncek (Eds.), Lecture Notes in Computer Science 8986, 188–199, 2015, https://doi.org/10.1007/978-3-319-19315-1 |
| [JP15a] | G. Jäger, M. Peczarski, The worst case number of questions in Generalized AB game with and without white-peg answers, Discrete Applied Mathematics 184, 20–31, 2015, https://doi.org/10.1016/j.dam.2014.10.032, 2013, https://arxiv.org/abs/1306.1713 |
| [JP15b] | G. Jäger, M. Peczarski, Bounding memory for Mastermind might not make it harder, Theoretical Computer Science 596, 55–66, 2015, https://doi.org/10.1016/j.tcs.2015.06.039 |
| [GMS15] | M. Grabowski, M. Marschall, W. Sirko, M. Dębski, M. Ziombski, P. Horban, Sz. Acedański, M. Peczarski, D. Batorski, K. Iwanicki, An experimental platform for quantified crowd, WiMAN 2015, 7th International Workshop on Wireless Mesh and Ad Hoc Networks, Las Vegas, NV, USA, August 3, 2015, Proceedings, IEEE, 2015 |
| [P17] | M. Peczarski, Comments on the Golden Partition Conjecture, Contributions to Discrete Mathematics 12 (1), 106–109, 2017, https://doi.org/10.11575/cdm.v12i1.62349 |
| [P18e] | M. Peczarski, Algorithm to prove formulas for the expected number of questions in Mastermind games, https://arxiv.org/abs/1808.03849 |
| [P19] | M. Peczarski, The worst balanced partially ordered sets—ladders with broken rungs, Experimental Mathematics 28 (2), 181–184, 2019, published on-line 6 October 2017, https://doi.org/10.1080/10586458.2017.1368050 |
| [P26] | M. Peczarski, Note on pancake sorting, Information Processing Letters 191, Article 106597, 2026, https://doi.org/10.1016/j.ipl.2025.106597 |
If you want a copy, please send an  .
.
| M. Peczarski, Sortowanie z minimalną liczbą porównań, Delta 11/2004 |
| M. Peczarski, (100)16 centów za błąd, Delta 1/2008 |
| M. Peczarski, Ile mikroprocesorów jest w tym pokoju?, Delta 5/2009 |
| M. Peczarski, How many microprocessors are there in this room?, Delta Special Issue 2012 |
| M. Peczarski, Złoty podział w sortowaniu, Delta 12/2013 |
| M. Peczarski, Sieć, Delta 1/2016 |
| M. Peczarski, Opóźnienia w STM32. Precyzyjne odmierzanie czasu w połączeniu z trybami oszczędzania energii, Elektronika Praktyczna 7/2010 i 8/2010. |
Results marked with [ICM] are obtained using computer resources of the Interdisciplinary Centre for Mathematical and Computational Modelling of the University of Warsaw.