Zadanie 1: DRZEWA (40 pkt)

Termin oddania zadania: 06.04.2003

Definicja

Niech T = (V, E) będzie drzewem. Zbiór wierzchołków D (niekoniecznie wszystkich) nazwiemy dominującym, gdy dla dowolnego wierzchołka v należącego do V, zbiór D zawiera v lub jednego z sąsiadów v (oczywiście może zawierać v i kilku jego sąsiadów). Poniżej przedstawiono dwa zbiory dominujące dla tego samego drzewa (na czarno oznaczono wierzchołki zbioru dominującego):

Treść zadania

Zadanie
Rozważmy drzewo z korzeniem, w którym każdy wierzchołek przechowuje dwie liczby całkowite: Maksymalna liczba synów wierzchołków w naszym drzewie nie jest określona. Napisz program, który:

Faza 0 (10 punktów)
Wczyta z pliku DRZ_IN.TXT opis struktury drzewa i zbuduje drzewo w pamięci komputera.

Faza 1 (10 punktów)
Znajdzie wierzchołek v taki, że suma kluczy jego potomków jest największa a następnie wypisze identyfikator znalezionego wierzchołka v do pliku DRZ_OUT_1.TXT. Uwaga ! Zakładamy, że każdy wierzchołek jest swoim własnym potomkiem.

Faza 2 (10 punktów)
Znajdzie dwa wierzchołki u i v takie, że u jest przodkiem v i różnica ich kluczy (tzn. |Klucz(u)-Klucz(v)|) jest największa. Następnie wypisze identyfikatory znalezionych wierzchołków do pliku DRZ_OUT_2.TXT.

Faza 3 (10 punktów)
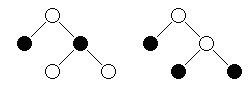
Znajdzie najmniejszy zbiór dominujący wczytanego drzewa i wypisze identyfikatory wierzchołków znajdujących się w tym zbiorze do pliku DRZ_OUT_3.TXT.

Pamiętaj, że Twój program powinien być efektywny czyli dla dowolnych danych wejściowych dawać odpowiedź po niezbyt długim czasie (nie więcej niż kilka sekund na przeciętnym komputerze). Dlatego zastanów się nad złożonością czasową poszczególnych faz swojego rozwiązania. Rozwiązania nieefektywne będą gorzej punktowane.

Wejście
W pierwszym wierszu pliku DRZ_IN.TXT znajduje się jedna liczba n, oznaczająca liczbę wierzchołków drzewa, n < 100000. Zakładamy, że identyfikatory wierzchołków są liczbami od 1 do n. Możemy założyć (choć nie jest to konieczne), że dowolny wierzchołek ma zawsze numer mniejszy niż jego potomkowie. W wierszu o numerze i+1 pliku DRZ_IN.TXT znajduje się opis wierzchołka o identyfikatorze i: dwie liczby naturalne p, k oddzielone spacją, gdzie p oznacza numer jego ojca a k klucz, -30000 < k < 30000. Jeśli p jest zerem, oznacza to, że dany wierzchołek jest korzeniem. Zakładamy, że plik DRZ_IN.TXT zawiera dane zapisane w poprawny sposób (opisany powyżej).

Wyjście
Pliki DRZ_OUT_1.TXT, DRZ_OUT_2.TXT, DRZ_OUT_3.TXT zawierają odpowiednie liczby oddzielone spacjami.

Przykład
Dla pliku DRZ_IN.TXT: 

6
0 10 
1 -10
1 15
3 0
3 -2
3 35
Poprawny plik DRZ_OUT_1.TXT może mieć postać: 
3
Poprawny plik DRZ_OUT_2.TXT powinien mieć postać: 
1 6
Poprawny plik DRZ_OUT_3.TXT może mieć postać: 
2 3

Forma rozwiązania zadania

Rozwiązanie powinno być napisane i przetestowane na komputerze. Program będący rozwiązaniem powinien być "aplikacją konsolową", co oznacza, żę nie powienien zawierać żadnych okien, powinien otwierać się w trybie tekstowym, czytać dane z pliku wejściowego, obliczać rozwiązanie i zapisywać je w pliku wyjściowym.
Najprościej jest napisać takie rozwiązanie w Turbo Pascalu, można jednak użyć delphi. Program w Delphi będzie wyglądał tak samo jak ten w Pascalu, musi zawierać jednak napis {$apptype console}.
Należy w tym celu wykonać następujące kroki (dla Delphi 5):
  1. Wybrać z menu głównego Delphi "New..."
  2. W okienku, które się pojawi wybrać "Console Application"
  3. Utworzony zostanie nowy projekt, skladajacy sie tylko z jednego pliku.
  4. Zapisac projekt pod nazwa "ban.dpr"
  5. Napisać rozwiązanie zadania w pliku "ban.dpr"
Natomiast dla wcześniejszych wersji Delphi:
  1. Utworzyć nowy projekt
  2. Usunąć z projektu plik formatki "Unit1.pas"
  3. Zapisać projekt pod nazwa "ban.dpr"
  4. zmienić treść pliku ban.dpr na następującą: 
    program ban;
uses 
  SysUtils;
{$apptype console}
begin
end.
  5. Napisać rozwiązanie zadania w pliku "ban.dpr"

Rozwiązania można przynieść na dyskietce, lub przesłać pocztą elektroniczną jako załącznik na adres: kowalik@mimuw.edu.pl

UWAGA! Proszę podpisywać rozwiązania (umieścić imię i nazwisko w pliku z rozwiązaniem) - także te wysyłane e-mailem !