Zadania przygotowawcze: przykłady zadań egzaminacyjnych

Egzamin 19.01.2002

Pliki .PS można oglądać i drukować za pomocą programu GhostView, a pliki .PDF za pomocą programu AcrobatReader. Oba programy można za darmo ściągnąć z sieci (AcrobatReadera np. z http://www.adobe.com/acrobat).

Zadanie 1 (struktury danych: stos)

Na początkowo pustym stosie s wykonano następujące operacje:

s.Push (1);
s.Push (2);
s.Pop;
s.Push (5);
s.Push (3);
s.Pop;
WeiteLn (s.Top);

Narysuj wygląd stosu po każdej z operacji i określ, jaka liczba zostanie wypisana przez program.

Zadanie 2 (struktury danych: drzewo BST)

Do początkowo pustego drzewa BST wstawiono kolejno następujące elementy:

3, 1, 5, 20, 23, 22, 88, 40

Zakładając, że użyto zwykłego algorytmu wstawiania (który nie zmienia położenia węzłów wcześniej wstawionych), narysuj drzewo BST powstałe po tym ciągu wstawień. Czy to drzewo jest doskonale wyważone ?

Zadanie 3 (programowanie dynamiczne)

Dane jest pewne słowo w długości n składające się z liter a, b, c, d, e, f, g, h, i, j (niekoniecznie wszystkich). Jeśli w słowie w występują obok siebie dwie takie same litery, możemy je usunąć a na ich miejsce wpisać literę następną lub poprzednią (w odniesieniu do porządku alfabetycznego), np:

słowo bb możemy zamienić na a lub c
słowo edbbc możemy zamienić na edac lub edcc
słowo aa możemy zamienić na b lub j
itd.

Napisz algorytm, który dla danego słowa w oblicza, czy za pomocą ciągu opisanych operacji można od słowa w dojść do słowa składającego się tylko z jednej litery. Jeśli jest to możliwe, Twój algorytm powinien wypisać wszystkie litery, które można w ten sposób otrzymać, wpp słowo "NIE", np:

dla w = edbbc prawidłowa odpowiedź jest "d f"
dla w = aaaa prawidłowa odpowiedź jest "a c d i"
dla w = aac prawidłowa odpowiedź jest "NIE"

Podpowiedź

Zadanie 4

Dane jest k list liczb całkowitych. Każda lista jest posortowana. Należy scalić te listy (połączyć w jedną posortowaną listę zawierającą wszystkie elementy list wejściowych). Złożoność czasowa nie powinna przekraczać O(n*logk), gdzie n = suma długości wszystkich k list (długość wynikowej listy). Podaj złożoność czasową i pamięciową swojego rozwiązania wraz z uzasadnieniem.

Podpowiedź

Zadanie 5

Niech T = (V, E) będzie drzewem. Zbior wierzchołków D (niekoniecznie wszystkich) nazwiemy dominującym, gdy dla dowolnego wierzchołka v należącego do V, zbior D zawiera v lub jednego z sąsiadów v (oczywiście może zawierać v i kilku jego sąsiadów). Poniżej przedstawiono dwa zbiory dominujące dla tego samego drzewa (na czerowno oznaczono wierzchołki zbioru dominującego):

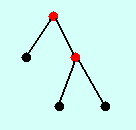
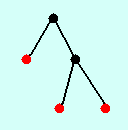
zbiór dominujący

Napisz algorytm, który dla danego drzewa (reprezentowanego w pamięci np. wg zasady lewy syn-prawy brat) znajdzie dowolny najmiejszy (pod względem liczności) zbior dominujący (można założyć, że w każdym wierzchołku przechowywany jest jego unikalny numer, a algorytm powinien wypisać numery wierzchołków dowolnego najmniejszego zb. dominującego). Podaj złożoność czasową i pamięciową swojego rozwiązania wraz z uzasadnieniem.

Podpowiedź

Zadanie 6

Algorytm sortowania nazwiemy antystabilnym, gdy dwa takie same elementy tablicy ustawiane są zawsze w odwrotnej kolejności niż na początku. Zmodyfikuj algorytmy:
a) InsertionSort (sortowanie przez wstawianie)
b) MergeSort (sortowanie przez scalanie)
tak, aby były antystabilne (zmiany powinny byc jak najmniejsze !).

Zadanie 7

Napisz algorytm, który dla danych liczb naturalnych c, n zwróci część całkowitą liczby log_cn
a) o złożoności O(lh(n)^2 * log_cn) = O (lh (n)³ / log(c)).
b^*) o złożoności O(lh(n)^2 (log₂log_cn) = O (lh (n)² * (loglog(n) - loglog(c)).

Podpowiedź do a

Podpowiedź do b

Ostatnia modyfikacja: 03/25/2003 08:52:20.